混合策略

---

是纯策略的某种加权组合，权数表达了选择纯策略的概率。

设有一含N个局中人的对策，S_i是局中人i(=1，2，…，N)的纯策略集。形式上，称任何满足：

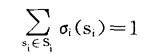
的函数σ_i∶S_i→[0，1]为局中人i的一个混合策略，其中σ_i(s_i)解释为i选择策略s_i的概率。

引入混合策略概念的主要好处在于它使得纳什均衡必定存在。考虑如图所示的标准型对策，它不存在纯策略纳什均衡。

记σ_A(上)=τ，σ_B(左)=λ，0≤τ，λ≤1。混合策略组或行动σ=(σ_A，σ_B)完全决定于τ，λ，就简记为(τ，λ)。

在(τ，λ)之下，局中人i的期望支付为

Eu_i(τ，λ)=τ[λu_i(上，左)+(1－λ)u_i(上，右)]+(1－τ)[λu_i(下，左)+(1－λ)u_i(下，右)]

其中i=A，B。若一个行动(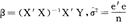，#)同时满足以下两个不等式：

Eu_A(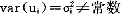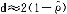，)≥Eu_A(τ，#)，对所有0≤τ≤1，

Eu_B(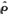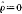，)≥Eu_B(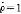，λ)，对所有0≤λ≤1，

则称(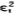，)为一个混合策略纳什均衡。

以支付矩阵的数据代入，得Eu_A(τ，λ)=(1－τ)(2λ－1)，Eu_B(τ，λ)=(1－λ)(3－4τ)。

容易验证，当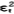=3／4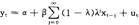，=1／2时，上述两不等式同时成立，因此行动(3／4，1／2)是一个混合策略的纳什均衡。