指两个随机事件的积事件的概率,等于其中一个事件的概率(此概率必须大于零)与另一事件在前一事件出现的条件下的条件概率的乘积。
设A、B为两个随机事件,则
P(AB)=P(A)·P(B/A)
=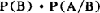
当A与B相互独立时,
P(AB)=P(A)·P(B)这个关系推广到n个事件A1,A2……An,则
P(A1A2……An)=P(A1)·P(A2/A1)·P(A3/A1A2)……
P(An/A1·A2……An-1)
由这个定理,可得下列两个推论:(1)某事件一次出现的概率为P,则连续n次都出现的概率为Pn(假如n次试验都是相互独立的);(2)n个独立事件,各个事件出现的概率分别为P1,P2,……Pn。则n个事件不出现的概率为(1-P1)(1-P2)……(1-Pn);n个事件至少有一个出现的概率为1-(1-P1)(1-P2)……(1-Pn)。
例如,假设96件产品中有5件是次品,依次抽取两件,问两件都合格的概率为多少?
解:设事件A为“第一次抽得合格品”,B为“第二次抽得合格品”。
显然,求的是积事件AB的概率P(AB)。
由乘法公式
P(AB)=P(A)P(B/A)
式中:P(A)、P(B/A)分别可求出:

故
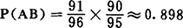
- 中国农业百科全书︱各种丝绸是什么意思
- 中国农业百科全书︱各种卵色是什么意思
- 中国农业百科全书︱各种茧色是什么意思
- 中国农业百科全书︱吐丝是什么意思
- 中国农业百科全书︱唐代印花绢裙(新疆吐鲁番阿斯塔那出土)是什么意思
- 中国农业百科全书︱唐代变体宝相花纹锦鞋(新疆吐鲁番阿斯塔那出土)是什么意思
- 中国农业百科全书︱唐代联珠对鸡纹锦 (新疆吐鲁番阿斯塔那出土)是什么意思
- 中国农业百科全书︱喜送蚕茧林孙杏摄是什么意思
- 中国农业百科全书︱喷雾补湿是什么意思
- 中国农业百科全书︱四川四边桑是什么意思
- 中国农业百科全书︱四川省农业科学院蚕业研究所是什么意思
- 中国农业百科全书︱国际蚕业会议代表参观马来西亚桑园是什么意思
- 中国农业百科全书︱土壤卷各分支编写组主编、副主编是什么意思
- 中国农业百科全书︱土壤卷编辑委员会是什么意思
- 中国农业百科全书︱坐缫是什么意思
- 中国农业百科全书︱外国人名译名对照表是什么意思
- 中国农业百科全书︱外宾参观西南农业是什么意思
- 中国农业百科全书︱学员在刈桑枝是什么意思
- 中国农业百科全书︱学员在进行显微观察是什么意思
- 中国农业百科全书︱学员在进行茧质调查是什么意思
- 中国农业百科全书︱小蚕饲育联合作业机是什么意思
- 中国农业百科全书︱尖柞是什么意思
- 中国农业百科全书︱尼洋河畔的古桑树,树龄1600年以上(西藏林芝县)是什么意思
- 中国农业百科全书︱山东桑粮间作是什么意思
- 中国农业百科全书︱山茶花(48 ‘大红球’)是什么意思
- 中国农业百科全书︱山茶花(49 ‘玛瑙’)是什么意思
- 中国农业百科全书︱山茶花(50 ‘花露珍’)是什么意思
- 中国农业百科全书︱山茶花(51 ‘玉美人’)是什么意思
- 中国农业百科全书︱山茶花(52 ‘金盘荔枝’)是什么意思
- 中国农业百科全书︱山茶花(53 ‘绛雪’(山茶树))是什么意思
- 中国农业百科全书︱山茶花(54 ‘金花茶’)是什么意思
- 中国农业百科全书︱帛画(局部)是什么意思
- 中国农业百科全书︱平原栽桑是什么意思
- 中国农业百科全书︱广东省农业科学院蚕业研究所是什么意思
- 中国农业百科全书︱彝族蜂桶是什么意思
- 中国农业百科全书︱捻丝是什么意思
- 中国农业百科全书︱摄食是什么意思
- 中国农业百科全书︱整理是什么意思
- 中国农业百科全书︱整经是什么意思
- 中国农业百科全书︱新疆桑田是什么意思
- 中国农业百科全书︱昆虫卷主要编辑出版人员是什么意思
- 中国农业百科全书︱昆虫卷各分支编写组主编、副主编是什么意思
- 中国农业百科全书︱昆虫卷编辑委员会是什么意思
- 中国农业百科全书︱月季(22 ‘春雨’)是什么意思
- 中国农业百科全书︱月季(23 ‘金秋’)是什么意思
- 中国农业百科全书︱月季(24 蔓性月季)是什么意思
- 中国农业百科全书︱月季(25 ‘月月红’)是什么意思
- 中国农业百科全书︱月季(26 ‘金桂飘香’)是什么意思
- 中国农业百科全书︱月季(27 ‘怡红院’)是什么意思
- 中国农业百科全书︱月季(28 ‘黄和平’)是什么意思
- 中国农业百科全书︱月季(29 ‘扶本’)是什么意思
- 中国农业百科全书︱月季(30 ‘蓝香’)是什么意思
- 中国农业百科全书︱月季(31 ‘香紫红’)是什么意思
- 中国农业百科全书︱月季(32 ‘杏花村’丰花月季)是什么意思
- 中国农业百科全书︱月季(33 ‘轮巴’聚花月季)是什么意思
- 中国农业百科全书︱月季(34 ‘红双喜’)是什么意思
- 中国农业百科全书︱朱红罗绵袍是什么意思
- 中国农业百科全书︱机械剪桑是什么意思
- 中国农业百科全书︱杜鹃花(15 露珠杜鹃)是什么意思
- 中国农业百科全书︱杜鹃花(16 羊踯躅杜鹃)是什么意思