有限差分与差商

---

设函数y=f(x)在结点x₀＜x₁＜…＜x_n(常取x_k=x₀+kh)处的值为y₀，y₁，…，y_n，即f(x_k)=y_k(k=0，1，2。…n)。

15．2．1 有限差分

向前差分：

一阶向前差分 △y_k=y_k+1－y_k

二阶向前差分 △²y_k==△y_k+1－△y_k

……………………………

m阶向前差分 △^myk=△^m－1y_k+1－△^m－1y_k

向后差分：

一阶向后差分 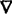y_k=y_k－y_k－1

二阶向后差分 ▽2y_k=▽y_k－▽y_k－1

……………………………

m阶向后差分 ▽^myk=▽^m－1yk－▽^m－1y_k－1

中心差分：

一阶中心差分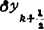=yk+1－yk

二阶中心差分 δ²yk=－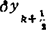

………………………………

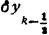
m阶中心差分

δ^my_k=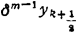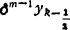－(m为偶数)

或δ^my_k+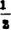=δ^m－1y_k+1－δ^m－1y_k(m为奇数)

三种差分间的关系：▽^kyk=△^ky₀；δ^2kyk=△^2ky_o；δ^2k+1y_k+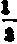=△^2k+1y。

15．2．2 差商(均差)

一阶差商 f(x_k，x_k+1)=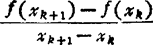

二阶差商 f(x_k，x_k+1，x_k+2)

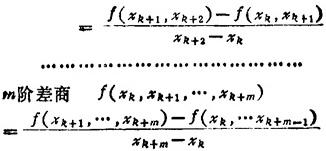
若f(x)在〔a，b〕上n次可微，x₀，x₁，…，xn是〔a、b〕内的(n+1)个不同点，则存在ξ(α＜ξ＜b)使得

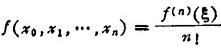
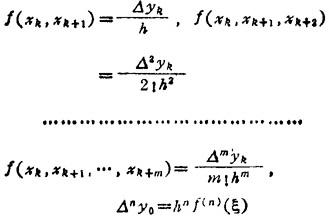
对于等距结点，差分、差商和导数间存在如下关系：