一种参数估计方法。
要求母体X具有确定形式的分布密度族{f(x,θ);θ∈H},其中θ=(θ1,…,θk)是待估计的未知参数向量。设(x1,…,xn)是子样(x1,…,xn)的一个观察值,那么子样(x1,…,xn)落在点(x1,…,xn)的邻域里的概率密度是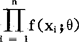 。这样,θ的变化会影响到
。这样,θ的变化会影响到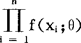 的大小的变化。直观上讲,既然在一次试验中得到了观察值(x1,…,xn),那么有理由认为子样落在该观察值(x1,…,xn)的邻域里这一事件是较易发生的,具有较大的概率,于是子样落在观察值(x1,…xn)的邻域里的概率密度应该达到最大。
的大小的变化。直观上讲,既然在一次试验中得到了观察值(x1,…,xn),那么有理由认为子样落在该观察值(x1,…,xn)的邻域里这一事件是较易发生的,具有较大的概率,于是子样落在观察值(x1,…xn)的邻域里的概率密度应该达到最大。
我们就选取使得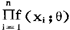 达到最大的参数值θ°作为θ的估计值,即θ°满足如下方程式:
达到最大的参数值θ°作为θ的估计值,即θ°满足如下方程式:
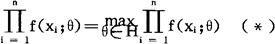
这样的θ°称为θ的最大似然估计,这一估计方法称为最大似然法。
在(*)式中求θ°,可用对数进行求解。
由于logx是x的单调函数,所以(*)式等价于
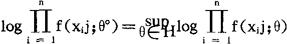
如果H是开集,且f(x;θ)关于θ可微,则(*)式的解θ°也满足下列方程:
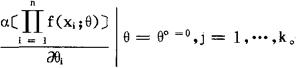
- 不知要领是什么意思
- 不知规是什么意思
- 不知言之人, 乌可与言; 知言之人, 默焉而其意已传。是什么意思
- 不知言,无以知人是什么意思
- 不知言,无以知人也。是什么意思
- 不知诗病,何由能诗是什么意思
- 不知该做什么好是什么意思
- 不知该怎么办是什么意思
- 不知该怎么办才好是什么意思
- 不知该怎么办,十分着急是什么意思
- 不知读书,则不知兵法是什么意思
- 不知谁是正宫娘娘是什么意思
- 不知谁是谁非是什么意思
- 不知谁氏子,独自作意气。是什么意思
- 不知谁照镜,挂在白云岑。万壑照成雪,梅花寒一林。是什么意思
- 不知谁让谁是什么意思
- 不知贵贱是什么意思
- 不知走哪条路是什么意思
- 不知起倒是什么意思
- 不知足是什么意思
- 不知足之蹈之,手之舞之。是什么意思
- 不知足地吃是什么意思
- 不知足的样子是什么意思
- 不知足者之忧,终身难解。是什么意思
- 不知足者,食费万钱,仍无下箸之处;知足者,粟邀五斗,犹念折腰而来。是什么意思
- 不知路途远是什么意思
- 不知轩屏侧,岁晚对袁安。是什么意思
- 不知轭在衡后是什么意思
- 不知轻重是什么意思
- 不知近水花先发,疑是经冬雪未消。是什么意思
- 不知近水花先发,疑是经冬雪未销是什么意思
- 不知还是井落在吊桶里,吊桶落在井里是什么意思
- 不知进退是什么意思
- 不知进退;不知深浅是什么意思
- 不知道东西南北是什么意思
- 不知道个厉害是什么意思
- 不知道事情的艰巨、严重是什么意思
- 不知道什么缘故是什么意思
- 不知道厉害是什么意思
- 不知道吃几碗干饭是什么意思
- 不知道哪块云彩有雨是什么意思
- 不知道哪头炕热是什么意思
- 不知道姜是辣的,盐是咸的是什么意思
- 不知道差多少是什么意思
- 不知道怎么好啦是什么意思
- 不知道怎么美好了是什么意思
- 不知道怎样着手是什么意思
- 不知道是什么东西是什么意思
- 不知道死活是什么意思
- 不知道深浅是什么意思
- 不知道演的是哪一出戏是什么意思
- 不知道盐怎么咸,醋怎么酸是什么意思
- 不知道眉眼高低是什么意思
- 不知道稀稠是什么意思
- 不知道自己有多大分量是什么意思
- 不知道臭是什么意思
- 不知道要告知什么是什么意思
- 不知道该怎么办是什么意思
- 不知道谁家坟里长大树是什么意思
- 不知道香臭是什么意思