普通最小平方法

---

一种最常用的回归系数估计法。

它的特点是：对于因变量与自变量的若干组观测值，按给定的函数形式确定因变量与自变量的回归式，使得因变量的回归值(以自变量的观察值代入回归式算出的因变量值)与因变量观测值之差的平方之和为最小。

例如，设有因变量Y与自变量X的n对观测值(Y_i，X_i)(i=1，…，n)，并设x与Y有线性关系Y=b₀+b₁x+u(其中u为零均值的随机变量)。

最小平方法就是求一直线

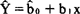
使得

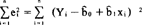
为最小。

为使上式达到极小，须使它对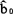和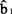的一阶编导数等于0，即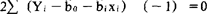

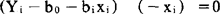
化简为：

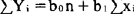
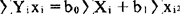
这个方程组称为最小平方法的“正规方程”。

解此方程得：

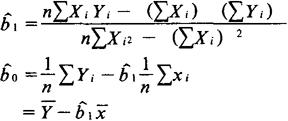
如果回归方程中的u是均值为0、具有常数方差、与自变量不相关、在各次观察中彼此不相关的随机变量，则用最小平方法得出的回归系数估量是无偏的；且在所有线性无偏估计量中，它的方差是最小的。

普通最小平方法因具有以上优良性质且计算简单而被广泛应用。普通最小平方法还是许多其它经济计量方法的基本组成部分。