支出函数

---

在消费者理论中，如果消费者有表示其偏好关系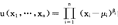的效用函数u(·)，则对于一个指定的效用水平u和价格p=(p₁，…，p_n)，支出函数是为了得到效用水平不低于u所必须的最小支出，即支出函数e(p，u)定义为：

e(p，u)=min{p·x|u(x)≧u}

对指定的收入水平w和价格p=(p₁，…，p_n)，间接效用函数是消费者可能达到的最大效用水平，即间接效用函数v(p，w)定义为：

v(p，w)=max{u(x)|p·x≦w}

如果偏好关系遵从局部不满足性假设(参见"偏好关系")，则支出函数和间接效用函数互为反函数。

例如设效用函数u(x₁，x₂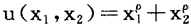)=xx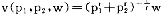^－α，则对应的支出函数e(p₁，p₂，u)=K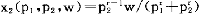pp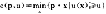^－αu，其中K为与α有关的常数。用w代替e(p₁，p₂，u)，用v(p₁，p₂，w)代替u，则容易从支出函数求出对应的间接效用函数v(p₁，p₂，w)=w／Kp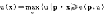p^－α。