常见的薄壳结构几何形状,有圆柱壳、圆锥壳、球壳、旋转壳等。薄壳受载变形后,如果中曲面上各点的法向位移均比薄壳厚度小得多,则称为薄壳的小挠度问题。
小挠度薄壳理论简化计算的基本假定:
❶ 平行于中曲面各面的法向正应力,比其它应力小得多,忽略不计。
❷ 变形前与中曲面垂直的线段,变形后仍为与中曲面垂直的直线,且长度不变。
薄壳受外力作用,在微元上的内力有两类:
❶ 使薄壳伸长或缩短的力,称为薄膜力,如图1.3-30(a)所示的Na,Nβ和Naβ。
❷ 使薄壳弯曲或挠曲的力,包括弯矩,扭矩与剪切力,如图1.3-30(b)所示的Ma,Mβ,Maβ、Qa和Qβ。
如果薄壳受均匀外力作用,壳的厚度和曲率没有突然变化,并且没有产生弯矩的边界条件(如与其它构件刚性联结),此时可以忽略弯矩、扭矩和剪力的影响。只有薄膜力作用的薄壳可以仅由静力学方法计算内力,这种简化计算的理论称为薄膜理论或无矩理论。
2.4.1 旋转薄壳的薄膜理论
若壳体中曲面是由一条曲线或直线绕某轴旋转而成的,则称为旋转壳。过旋转轴的平面与中曲面的交线称为子午线。垂直旋转轴的平面与中曲面的交线是一个圆,称为平行圆。
旋转壳受轴对称载荷作用时,其微元内力,如图1.3-31所示,有:沿子午线方向的单位长度拉力或压力NΦ;沿平行圆方向的单位长度拉力或压力Nθ;沿子午线切线方向的单位面积载荷分量p1;沿中曲面法线方向的单位面积载荷分量pn。
旋转壳薄膜理论的平衡方程为:
由上述二个平衡方程可以求解二个未知内力Na和Ns。
表1.3-31列出各种旋转壳受轴对称载荷作用时薄膜力和变形的计算公式。
表1.3-31 轴对称旋转壳薄膜力和变形计算公式
当Nx=0,即沿x方向没有拉力或压力时,位移与应变的关系是:
Mθ=-D(Kθ+μKΦ)
边界条件:
固定边:θ=0,ε2=0(u=0) (1.3-72a)
自由边:MΦ=0,NΦ=0(或QΦ=o) (1.3-72b)
封顶壳:在Φ=0处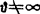 ,
,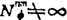 (1.3-72c)
(1.3-72c)
轴对称边界载荷作用下冠状球壳的内力和边缘处径向位移δ与转角φ的计算公式见表1.3-35;轴对称边界载荷作用下圆锥壳的内力和边缘处径向位移δ与转角ψ计算公式见表1.3-36。
表1.3-35 冠状球壳内力和边缘变形计算公式
半球壳和圆柱壳半径为R;厚度相同,为t;材料相同(弹性模量E和泊松比μ);承受内压力p。
先将半球壳与圆柱壳分开,按无矩理论计算。
由表1.3-31查得:
半球壳
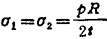
与圆柱壳连结的球壳端部,半径增大
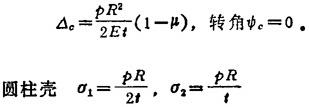
与半球壳连结的圆柱壳端部,半径增大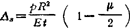 ,转角φs=0。
,转角φs=0。
由此可见,由薄膜应力产生的这两部分半径增大的差值为:
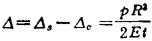
实际上,半球壳与圆柱壳是连续的,它是通过接合处单位周长的剪力Q0和弯矩Mo的相互作用而保持在一起的。这些相互作用力和力矩将使半球壳和圆柱壳在接合处附近引起局部弯曲应力。由表1.3-35和表1.3-32可以算出,当半球壳(Φo=90°)和长圆柱壳的半径R和厚度t相同时,在接合处两种壳由剪力Q0产生的径向位移和转角相同。因此,当Mo=0而Qo值能使圆柱壳边缘产生挠度为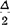 时,就能满足两种壳在接合处的变形连续条件。由表1.3-32得到
时,就能满足两种壳在接合处的变形连续条件。由表1.3-32得到
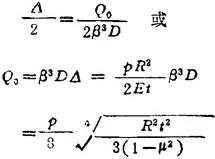
当Q0值求出后,即可由表1.3-32求得圆住壳离接合处距x的任意点纵向应力:
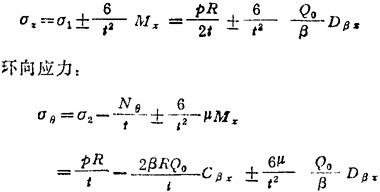
- 苦丁子咸是什么意思
- 苦丁茶是什么意思
- 苦丁茶叶是什么意思
- 苦丁香是什么意思
- 苦上加苦是什么意思
- 苦上加苦莫奈何是什么意思
- 苦不剌唧是什么意思
- 苦不可言是什么意思
- 苦不叽是什么意思
- 苦不咭是什么意思
- 苦不唧儿是什么意思
- 苦不唧儿的是什么意思
- 苦不啧啧是什么意思
- 苦不堪言是什么意思
- 苦不堪言;乐不可支是什么意思
- 苦不拉唧是什么意思
- 苦不拉唧儿是什么意思
- 苦不溜丢儿是什么意思
- 苦不聊生是什么意思
- 苦不胜言是什么意思
- 苦不辣是什么意思
- 苦与乐是什么意思
- 苦业是什么意思
- 苦丧是什么意思
- 苦丩丩是什么意思
- 苦中作乐是什么意思
- 苦中取乐是什么意思
- 苦中寻乐是什么意思
- 苦中寻乐苦中取乐是什么意思
- 苦中有乐是什么意思
- 苦中苦是什么意思
- 苦主是什么意思
- 苦乐是什么意思
- 苦乐不均是什么意思
- 苦乐主义是什么意思
- 苦乐之境是什么意思
- 苦乐时差与地差是什么意思
- 苦乐相寻昼夜间,灯光那有天明在。是什么意思
- 苦乐观是什么意思
- 苦乡绮梦录是什么意思
- 苦了一辈子是什么意思
- 苦了三年,岛于一朝是什么意思
- 苦了大嘴是什么意思
- 苦了大嘴了是什么意思
- 苦了巴叽是什么意思
- 苦争恶战是什么意思
- 苦事是什么意思
- 苦于是什么意思
- 苦于炎热是什么意思
- 苦井是什么意思
- 苦人儿是什么意思
- 苦人所难是什么意思
- 苦仁儿是什么意思
- 苦仁(人)儿是什么意思
- 苦今累明是什么意思
- 苦他嫑是什么意思
- 苦他巴是什么意思
- 苦伏竹是什么意思
- 苦会是什么意思
- 苦伪是什么意思