弹性力学基础

---

2．1．1 应力

一点的应力状态：在oxyz直角坐标系中，可用σ_x、σ_y、σ_z和τ_xy、τ_yx、τ_zx、t_yx、τ_ey、τ_xz九个应力分量表示一点的应力状态，如图1．3－26所示。

过一点任意斜截面的应力：设任意斜截面ABC上总应力S_N在坐标轴方向分量为X_N、Y_N和Z_N，如图1．3－27所示，则有

XN=1σ_x+mτ_yx+nτ_zx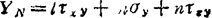

ZN=lτ_xz+mτ_yz+nσ_z

总应力在法向、切向的分量分别为

σN=l²σ_x+m²σ_y+n²σ_z+2Imτ_xy+2mnτ_yz+2nlτ_zx

平衡(运动)方程：在直角坐标系中，平衡(运动)方程为

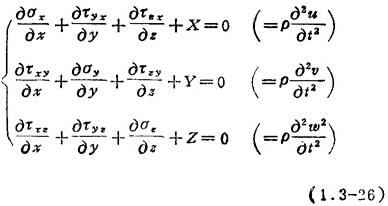
式中 X、Y、Z分别为单位体积力在坐标轴上投影。

边界条件：

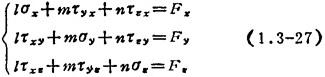
式中 F_z、F_y、F_z为单位面积上面力分量。

2．1．2 应变

应变与位移的关系——(直角坐标系中)几何方程

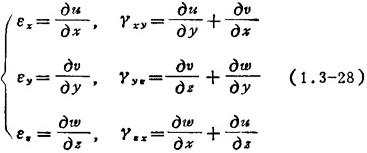
式中 u、v、ω为位移分量；ε_z、ε_y、e_e和γ_xy、γ_yz、γ_zx为应变分量。

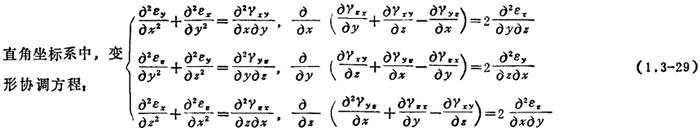
2．1．3 应力应变关系——物理方程

对于各向同性材料，物理方程可表示为如下形式。

以应力分量表示应变分量：

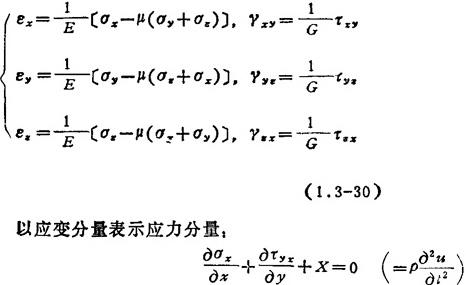
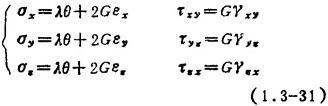
式中 E为弹性模量；G为剪切弹性模量：μ为泊松比；θ=ε_x+ε_y+e_z，为体积应变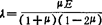；，为拉梅常数。

2．1．4 平面问题的基本方程和边界条件

弹性体的平面问题是空间问题的特例。此时弹性体的几何参数和所受外力只是x、y的函数，与z坐标无关。平面问题又分为平面应力问题和平面应变问题。

(1)平面问题的基本方程

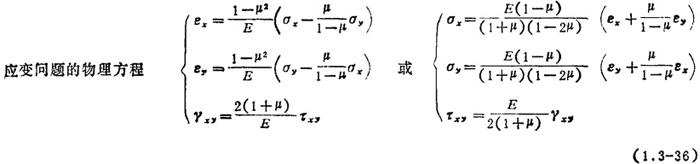
(2)平面问题的边界条件

位移边界条件(在Su上)：“=“，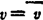

应力边界条件(在S_a上)：｛lσ_x+mτ_yr=P_xlτ_xy+mσ_y=F_y (1．3－37)

(3)平面问题的基本解法

位移法：以位移为基本未知量，其基本方程为

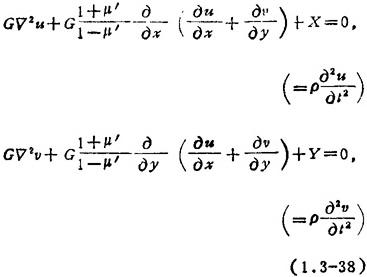
式中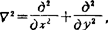为拉普拉斯算子：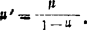

应力法：以应力为基本未知量，应力函数为φ，其基本方程为

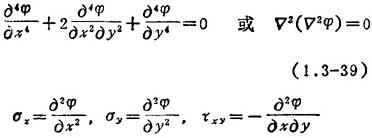
2．1．5 平面问题常用应力公式

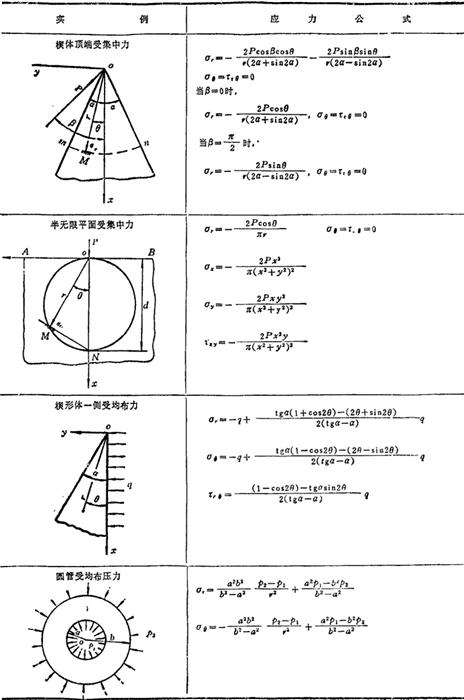
见表1．3－26。

表1．3－26 几种平面问题的应力公式

2．1．6 接触应力问题

两个互相接触的物体由于挤压产生的应力，称为接触应力。在接触处不允许自由变形，常呈三向应力状态。对于滚珠轴承、滚柱轴承、齿轮等零件进行强度计算时，应主要考虑接触应力。

根据弹性理论分析，一般情况下，接触面为椭圆面，长、短半轴分别为a、b，根据两接触物体的形状和材料性质可以求出a、b的数值。最大接触应力σ_max发生在接触面中心，其值为

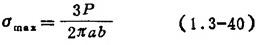
接触应力的强度校核，应采用第三或第四强度理论(见1．1．4中表1．3－5)。

几种常见接触应力的计算公式见表1．3－27。

表1．3－27 确定两个物体接触应力和参数的计算公式

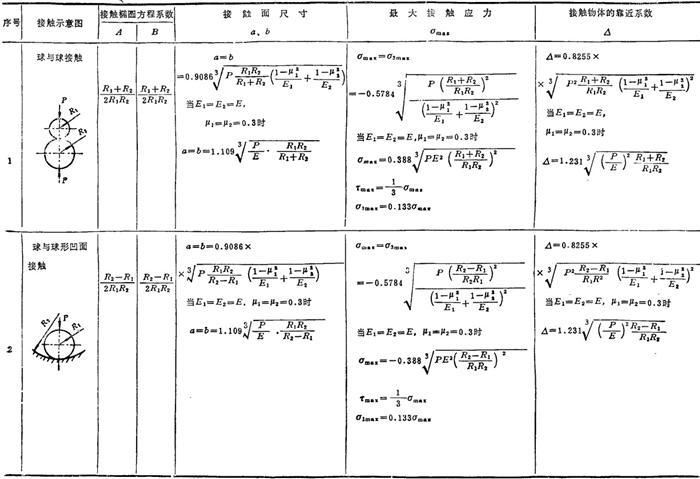
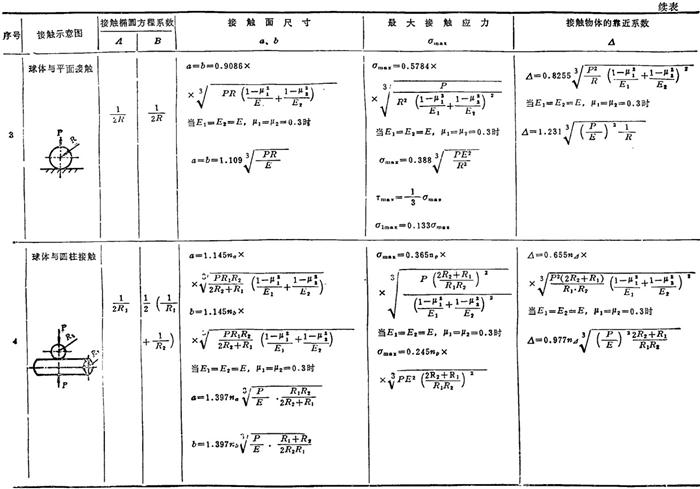
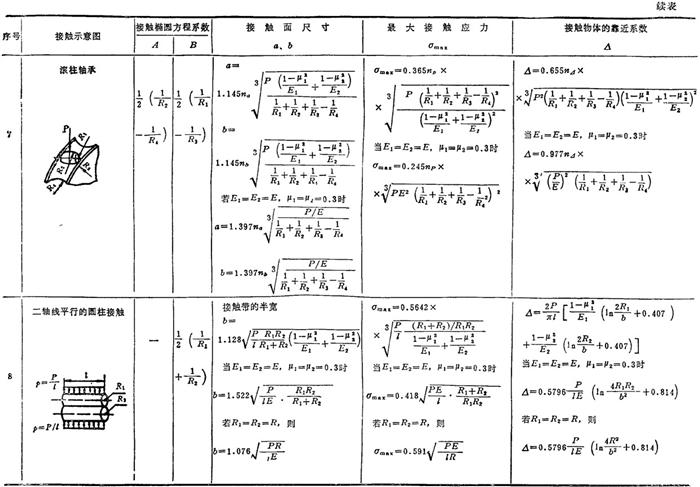
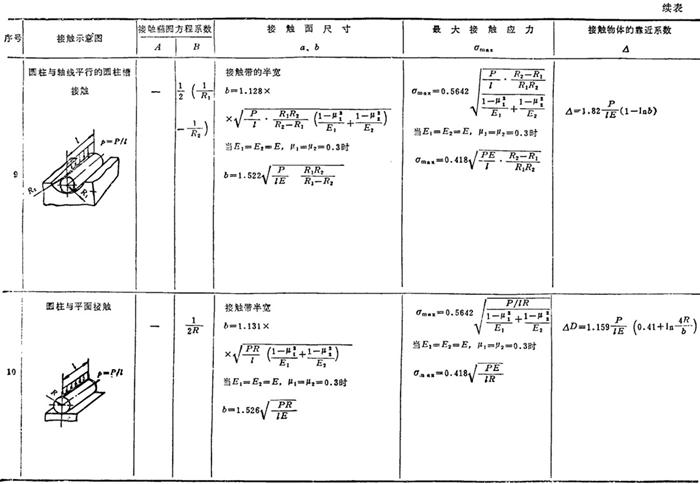
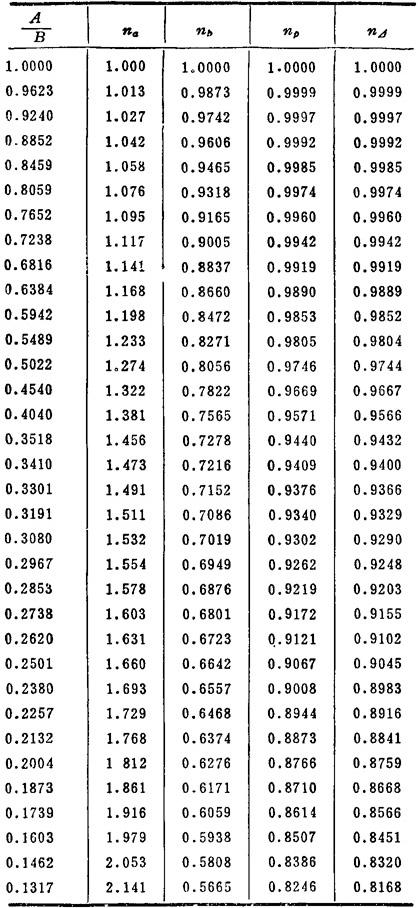
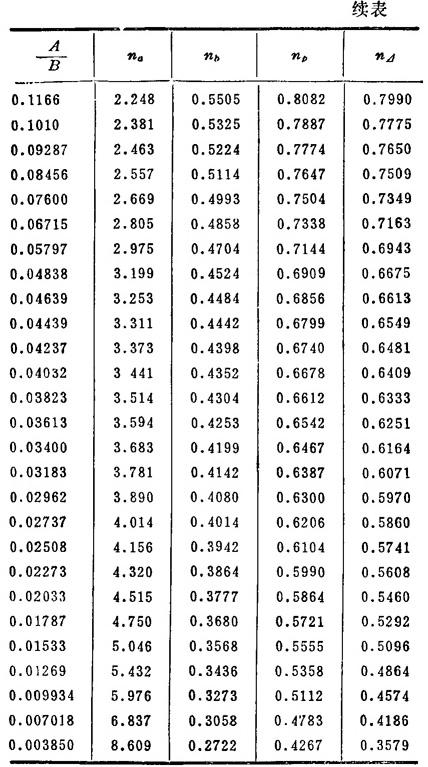
注：表中系数n_n、n_b、nP和n_⊿与A／B有关，见表1．3－28。

表1．3－28 n_a、n_b、n_p、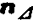的计算值