平行公理的推论

---

如果两条直线都与第三条直线平行，那么这两条直线互相平行．

注意 如果a∥c，b∥c，那么a∥b，说明平行线具有传递性

例1 下面说法中正确的个数是( )．

❶ 同一平面内不相交的两条直线一定平行．

❷ 同一平面内不相交的两条射线一定平行．

❸ 同一平面内不相交的两条线段一定平行．

A．0 B．1

C．2 D．3

答 B．

[解析] 两条线段或两条射线平行，是指它们所在的直线平行；两条线段或射线不相交，不能说它们所在的直线就不相交，故❷ 和❸ 不正确，故应选B．

例2 在同一平面内，直线l₁与l₂满足下列条件，写出与其对应的位置关系：

(1)l₁与l₂没有公共点，则l₁与l₂＿＿．

(2)l₁与l₂有一个公共点，则l₁与l₂＿＿．

(3)l₁与l₂有两个公共点，则l₁与l₂＿＿

答 (1)平行．(2)相交．(3)重合(是一条直线)．

例3 如图，已知AB∥CD，EF与AB交于点O，EF与CD平行吗?为什么?

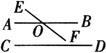
答 不平行．

理由：若EF与CD平行，由AB∥CD根据“如果两条直线都与第三条直线平行，那么这两条直线互相平行”可以得到AB∥EF，这与条件“EF与AB交于O点”矛盾，因此EF与CD相交．

例4 已知PA∥l，PB∥l，所以PA与PB重合，其理由是( )．

A．过两点有且只有一条直线

B．过一点只能作一条平行线

C．经过直线外一点有且只有一条直线和这条直线平行

D．如果两条直线都和第三条直线平行，那么这两条直线互相平行

答 C．