平均差

---

各个变量值对其算术平均数的平均离差。

由于离差总和恒等于零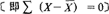，所以计算平均差时，采用离差的绝对值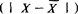。平均差越大，说明各标志值与平均数的离差越大；反之，平均差越小，说明各标志值的变动度越小，平均数的代表性越强。

计算平均差的公式，分为简单平均式和加权平均式两种。

1．简单平均式。

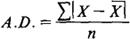
式中，A、D、代表平均差(其余符号的意义见平均指标条)。

例如，有两组工人，他们的月工资额如下：

甲组：50，60，70，80，90

乙组：60，65，70，75，80

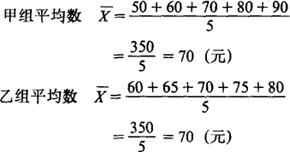
甲组的平均差是：

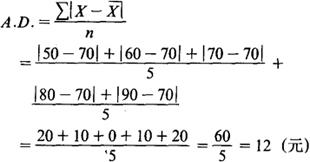
用同样的方法得乙组的平均差为：

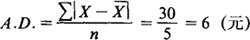
这就是说，在甲乙两组工人平均工资相等(均为70元)的情况下，甲组的平均差(12元)大于乙组平均差(6元)。

由此表明，甲组平均数的代表性不如乙组。

2．加权平均式。

在资料经过分组，形成分配数列时，应采取加权平均式。其公式为：

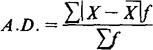
假设某企业200个职工的工资资料如下：

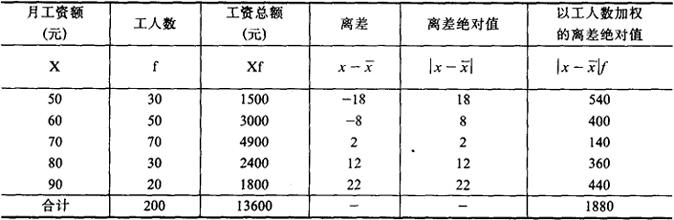
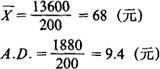
计算表明，该企业职工的月平均工资额为68元，与各个人的月工资额平均相差9．4元。