导数与微分的应用

---

7．7．1 函数存在极值的条件

若f′(x₀)=0或不存在，f′(x)通过x₀时变号，且f(x)在x₀点连续，则当x渐增过x₀时f′(x)由(+)变(－)，则f(x₀)为极大值；当x渐增过x₁时f′(x)由(－)变(+)，则f(x₀)为极小值。

若f′(x₀)=0，且f″(x₀)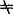0，则f(x₀)为极值；当f″(x₀)＜0时，f(x₀)为极大值；当f″(x₀)＞0时，f(x₀)为极小值。

对于多元函数f(P)=f(x、y、z，…t)，在点P₀(x₀，y₀，z₀，…t₀)处若满足：

❶ 必要条件：各个一阶偏导数都存在，且

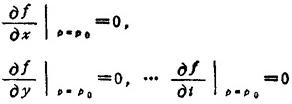
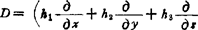
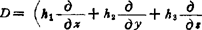
❷ 充分条件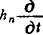：)²f当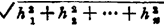甚小时，若D恒为正值，则f(P₀)为极小值；若D恒为负，则f(P₀)为极大，

7．7．2 曲线的凸凹性及拐点

在〔a，b〕上f″(x)存在。若f″(x)＞0，则曲线上凹，若f″(x)＜0，则曲线上凸；若f″(x₀)=0，且当x渐增通过x₀时f″(x)变号，则点(x₀，f(x₀))为拐点。