多项对数单位模型

---

对数单位模型的每个个体只有两项选择，若每个个体都面临多项选择，则模型为多项对数单位模型。

假设有J项选择，第i个个体选择了第k项选择的概率为：

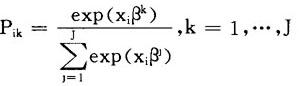
定义变量d_ik，若第i个个体选择了第k项选择，则d_ik=1，否则，d_ik=0。于是对数似然函数为：

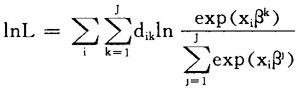
显然，若β=(β¹，β²，…，β^J)使得对数似然函数最大化，则β+c=(β¹+c，β²+c，…，β^J+c)也然(c为任意常数)。所以，必须对参数施加约束，不妨设β¹=0。于是

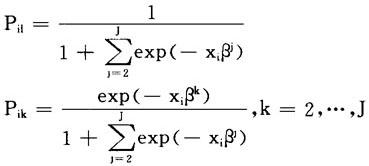
这样，就可得到惟一的参数最大似然估计。

使用过这种模型的情形包括：个体选择就业，高考生选择学校以及消费者在几个商业区中选择到哪个区去购物等。在上述各种情况下，决策者都必须从一组有限的离散备选方案中选择一个行动。