多变量回归模型

---

指有多个解释变量的回归模型。

一般说，有k个解释变量的线性回归模型可表示为：

Y_i=β₀+β₁X_1i+β₂X_2i+…+β_kX_ki+u_i

i=1，2，…，n

此处Y为应变量(或被解释变量)，X₁，X₂，…，X_k为自变量(或解释变量)，u为随机扰动项，β₀，β₁，…，β_k为待定参数。下标i表示第i次观测。

为了计算方便，通常使用矩阵表达式：

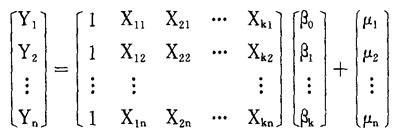
简写为Y=Xβ+μ，其中Y、X、β分别表示相应的向量或矩阵。

如果模型符合经典线性回归模型的假定，那么可以用普通[最小二乘法]计算出β₀，β₁，…，β_k的估计值，用矩阵表示计算公式如下：

β=(X′X)^－1X′Y

此处X′表示X的转置矩阵。估计的回归模型为：

Y=Xβ

经过统计检验、经济意义检验和计量经济学二级检验，如果模型成立，那么就可以用于经济分析和预测了。

对于违反经典线性回归模型假定的情况，参见[最小二乘法]中广义最小二乘法部分。

对于非线性模型，一部分可以化为线性模型来解；另一部分不能化为线性模型的，可用迭代法在计算机上求解，某些软件如TSP等，有估计非线性回归模型的命令，可以很方便地求解。