因子分析

---

最初由斯皮尔曼(Spearman，C．)1904年提出。

这是一种多元统计分析方法，其目的是为了减少用于描述事物状态的指标的维数，从而易于概括出该事物的本质。例如，在用p个指标X_i(i=1，2，…，p)描述事物的状态来研究一组指标的结构时，可以通过用尽可能少的且不可观测的变量(公共因子)来描述这些可观测的p个指标的相关模型，以便减少所考虑问题中的指标维数。

设有方程式：X_i=C_i1Z₁+C_i2Z₂+…+C_isZ_s+ε_i表示指标X的因子结构。

其中：X_i(i=1，2，…，p)具有零均值、单位方差；

Z_k(k=1，2，…，s)为公共因子，具有零均值、单位方差、互不相关；

C_ik(i=1，2，…，pk=1，2，…，s)称为"载荷"；

ε_i(i=1，2，…，p)为特定因子，具有零均值、单位方差、互不相关，并且与Z_k也互不相关。

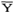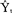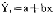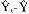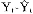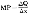假定公共因子Z_k对X各分量的总影响是：D=C_k+C_k+…+C_k，X_i对公共因子的依赖程度为：E=C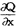+C+…+C。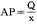

因子分析就是要选取一组公共因子Z_k(k=1，2，…，s)，使得Z_k的个数小于变量X_i(i=1，2，…，p)的个数，即s＜p，且s尽可能的小，以便提出一个简要的模型。

有关因子分析的理论和模型目前还不是很完善。比如，载荷矩阵C=(C_ik)不具惟一性，它可用矩阵CM替代(M是正交矩阵)。

这就需要在实际中选择合适的M，来简化因子结构，以便能更好地解释其结果。

因子分析应用广泛，在心理学、经济学、医学、农业和其他社会科学领域都有很好的应用。