非线性规划
见“数学”中的“非线性规划”。
非线性规划
见“规划论”。
非线性规划Nonlinear Programming
研究求解非线性规划问题的理论和方法。在数学模型中的约束条件方程和目标函数不全是线性函数的规划问题被称为非线性规划问题。由于数学模型构成的不同及非线性函数的复杂性,尚没有一个统一的、有效的方法来求解任何形式的非线性规划问题,只能对不同类型的问题给出不同的解法。并且只有当函数具有某种特性时,才能得到较满意的解。求解非线性规划的方法很多, 主要有黄金分割法、切线法(牛顿法)、抛物线逼近法、梯度法 (最速下降法)、共轭梯度法、变尺寸法、消元法、拉格朗日乘子法、罚函数法以及用线性规划逐步逼近非线性规划等方法。
非线性规划Non-Linear Programming
当目标函数或是约束条件中有至少一个是非线性函数时的规划问题为非线性规划。非线性规划的形式为:
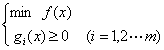
与线性规划不同,非线性规划并没有一个固定的解法,这是由于非线性规划可能的形式太多,如二次函数、指数函数和三角函数等等。非线性规划又可以划分不同的类型,针对其不同特点可采用不同的解法。
例:已知一段绳长1米,将这段绳围成一长方形,求如何围可使其面积最大?
解:设所围长方形长宽分别为x1,x2,则
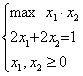
这就是一个简单的非线性规划模型。对于最简单的单变量非线性规划,如
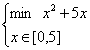
可以采用“爬山法”。做法是:在可行区域中任取一点(记为x0),向左或向右(随机决定)以一定步长迈出一步(记为x1,设是向左走的,且步长为d,则x1=(x0-d)。比较x1与x0处的目标函数值,若在x1处较小,则表明走对了,下一步仍朝这个方向走一步,否则表明方向走反了,下步应朝另一个方向走一步。这样无论初始点选在哪里,最终都能找到最优解。对比一下一个站在山腰上的人,他想走到峰顶,然而由于树木森森,他只能看到附近的地势,于是他将选择向高走一段,再观察哪儿更高以选择下一步的走向。显然爬山者要能爬到山顶的话,他得确信这座山只有一个峰,否则他很有可能会走到矮的那个峰去了。爬山法以及其他一些求解一元非线性规划的方法是求解一般非线性规划问题的基础,其求解的效率对整个问题求解的效率影响很大。如求解无约束非线性规划问题的最速下降法,其解法如下:先任取一个可行域中的点,按一定规则选取使目标函数下降最快的方向,在这个方向上寻找一点,使这一点的目标函数值最小,由于要找的点与初始点在一条已知的直线上,这时多元非线性规划问题就转化为求解一元非线性规划问题。总之,非线性规划的解法是试图将复杂的问题转化为简单的问题,再从简单的问题着手。
非线性规划
在数学规划中,目标函数和约束条件方程都可以是线性或非线性方程,如果有一个或多个目标函数或约束条件是非线性函数,就是非线性规划。从数学方面说,非线性规划就是一元或多元非一次代数方程组,在有约束或无约束的条件下求极值(最大值或最小值)的问题。线性规划是非线性规划的一个特例。在本世纪50年代以后,线性规划得到广泛应用,由于很多问题用线性规划处理只是获得近似解,非线性规划成了60年代以来重要的研究方面。目前对非线性规划还没有统一的解法,往往要灵活运用各种数学解析方法,运算比较复杂。非线性规划的应用比较广泛,如机械设计、电力网络管理、城市水源计划等方面的最优化问题。也可以用于宣传工作的设计。
非线性规划Non-Liear Programming
即目标函数或约束方程中存在一个或多个非线性函数的规划。非线性规划问题的数学模型通常也包括目标函数和约束条件两部分,即:
Max(Min)f(x)
hi(x)=0 i=1,2,…,m
gj(x)≥(≤)0 j=1,2,…,1
非线性规划
一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。20世纪50年代初,库哈(H.W.Kuhn) 和托克 (A.W.Tucker) 提出了非线性规划的基本定理,为非线性规划奠定了理论基础。这一方法在工业、交通运输、经济管理和军事等方面有广泛的应用,特别是在“最优设计”方面,它提供了数学基础和计算方法,因此有重要的实用价值。非线性规划问题用数学模型表示就是:
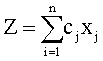
- 李文忠是什么意思
- 李文忠是什么意思
- 李文忠公全集是什么意思
- 李文恭公文集是什么意思
- 李文恭公行述是什么意思
- 李文恭公诗文集是什么意思
- 李文悌是什么意思
- 李文成是什么意思
- 李文成是什么意思
- 李文斋是什么意思
- 李文明是什么意思
- 李文明是什么意思
- 李文来是什么意思
- 李文杰是什么意思
- 李文杰是什么意思
- 李文杰是什么意思
- 李文林是什么意思
- 李文林是什么意思
- 李文林是什么意思
- 李文森是什么意思
- 李文森是什么意思
- 李文楷是什么意思
- 李文楷是什么意思
- 李文楷是什么意思
- 李文正公手书东祀录略卷是什么意思
- 李文求是什么意思
- 李文汉是什么意思
- 李文汉是什么意思
- 李文洁遗墨跋是什么意思
- 李文浩是什么意思
- 李文浩是什么意思
- 李文海是什么意思
- 李文清是什么意思
- 李文渊是什么意思
- 李文源是什么意思
- 李文炤是什么意思
- 李文炳是什么意思
- 李文炳是什么意思
- 李文烈是什么意思
- 李文煌是什么意思
- 李文照是什么意思
- 李文熙是什么意思
- 李文珊是什么意思
- 李文瑞是什么意思
- 李文生是什么意思
- 李文甫是什么意思
- 李文甫是什么意思
- 李文甫是什么意思
- 李文田是什么意思
- 李文田是什么意思
- 李文田是什么意思
- 李文田是什么意思
- 李文益是什么意思
- 李文範是什么意思
- 李文芳是什么意思
- 李文芳陷害赵玉贞是什么意思
- 李文英是什么意思
- 李文茂是什么意思
- 李文茂是什么意思
- 李文范是什么意思