刚体平面平行运动的分析方法

---

刚体作平面平行运动时，刚体中任何一点始终在平行于某一固定平面的平面内运动，因此研究刚体这种运动，只需研究刚体中任一与该固定平面平行的任一截面的运动即可。

刚体的平面平行运动可视为整体的平动(可由质心的运动来标志)反绕通过质心的与该固定平面正交的轴的转动的合成。刚体上任一点A在t时刻的瞬时速度可写出为：

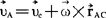
式中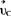为质心的瞬时速度，ω为瞬时角速度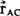，为A点相对于质心c的位矢。

若取该固定平面为XY平面，则本情况下该矢量式的分量式为

V_AX=V_CX－ω_Z(Y_A－Y_C)

V_AY=V_CY+ω_Z(X_A－X_C)

由此还可求知瞬时转动中心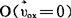的位置为

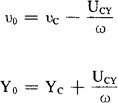
根据质点组的动量及动量矩定理，可知作平面平行运动的刚体的动力学方程为

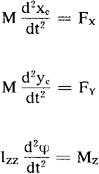
式中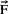为合外力，M_z为对质心的外力矩的Z轴分量，I_zz为该刚体绕通过质心的Z轴的转动惯量。此方程中的外力应包括约束力，因约束力一般为未知的，而描述该刚体运动的独立变量是三个(即X_C、Y_C及φ)，故还需加入限制运动的约束条件才能求解。