1.2.1 基本力系的简化
(1)汇交力系的简化
各力作用线相交于一点的力系称为汇交力系。汇交力系总可简化(合成)为合力。合力的大小和方向等于汇交力系主矢的大小和方向,合力的作用线过此汇交力系的汇交点。由合矢量的投影定理知,合力R在直角坐标轴上的投影等于各力在相应轴上投影的代数和,即
(2)其它力系简化实例
例1.2-1 如图1.2-6所示,在边长为α的正方形平板上作用著 ,
, ,
, 三力,各力的大小均为P。试求此三力的最简简化结果。
三力,各力的大小均为P。试求此三力的最简简化结果。
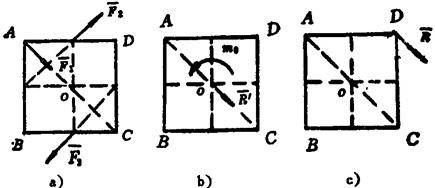
图1.2-6 力系简化实例一
解:计算力系主矢
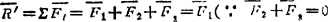 )选取Ο为矩心,计算力系主矩
)选取Ο为矩心,计算力系主矩
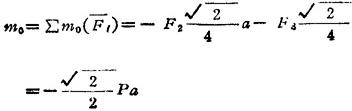
可见力系可简化为作用于O点的一个力和一个力偶(图1.2-6b)。
由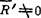 ,
,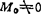 ,可知力系还可进一步简化为一合力R。由
,可知力系还可进一步简化为一合力R。由
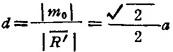
可知合力作用线过正方形顶点D(图1.2-6c)。其合力矢为
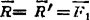
例1.2-2边长为a的正方体上作用二等值力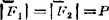 ,其作用线位置和方向如图1.2-7(a)所示。试求此二力的最简简化结果。
,其作用线位置和方向如图1.2-7(a)所示。试求此二力的最简简化结果。
解:建立如图坐标系Oxyz。计算力系的主矢
计算力系对O点的主矩
显而易见,由 知,
知, 和
和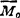 不垂直,故力系最简结果为一力螺旋。
不垂直,故力系最简结果为一力螺旋。
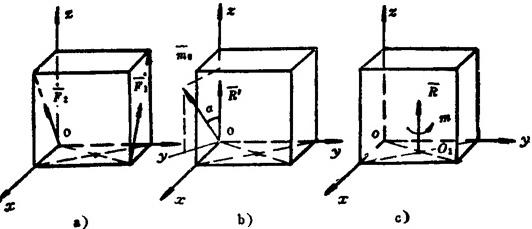
图1.2-7 力系简化实例二
由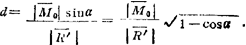 其中
其中
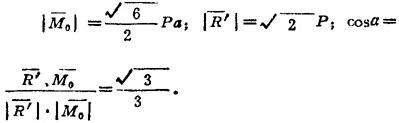
故代入上式化简可得
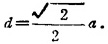
可知力螺旋的中心轴过底面中点O1。力螺旋的力矢和力偶矩矢分别为(图1.2-7(c)):
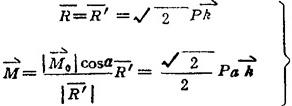
- 邹庭望墓是什么意思
- 邹延龄是什么意思
- 邹建军是什么意思
- 邹建平是什么意思
- 邹开清是什么意思
- 邹开良是什么意思
- 邹式金是什么意思
- 邹彦吉是什么意思
- 邹律是什么意思
- 邹德华是什么意思
- 邹德忠是什么意思
- 邹德骏是什么意思
- 邹必显是什么意思
- 邹必诚是什么意思
- 邹忆青是什么意思
- 邹忌是什么意思
- 邹忌巧对淳于髡是什么意思
- 邹忌窥镜是什么意思
- 邹忌讽齐威王纳谏是什么意思
- 邹忌讽齐威王纳谏(齐策一)是什么意思
- 邹忌讽齐王是什么意思
- 邹忌讽齐王纳谏是什么意思
- 邹忌讽齐王纳谏(《战国策》)是什么意思
- 邹志夔是什么意思
- 邹志奋是什么意思
- 邹志安是什么意思
- 邹志完是什么意思
- 邹志诚是什么意思
- 邹志贤是什么意思
- 邹忠倚是什么意思
- 邹忠桂是什么意思
- 邹恒泰是什么意思
- 邹愚谷是什么意思
- 邹慧君是什么意思
- 邹慰祖是什么意思
- 邹承鲁是什么意思
- 邹振先是什么意思
- 邹振清是什么意思
- 邹振祥是什么意思
- 邹搜是什么意思
- 邹敏是什么意思
- 邹敏初是什么意思
- 邹敬芳是什么意思
- 邹敬铭是什么意思
- 邹文怀是什么意思
- 邹文楷是什么意思
- 邹文樵是什么意思
- 邹文沅是什么意思
- 邹文海是什么意思
- 邹文盛智歼苗寇是什么意思
- 邹文苏是什么意思
- 邹斌元是什么意思
- 邹斯颐是什么意思
- 邹新垓是什么意思
- 邹方鲁是什么意思
- 邹日明是什么意思
- 邹昌炽是什么意思
- 邹明是什么意思
- 邹明富是什么意思
- 邹明理是什么意思