闭区间上连续函数的基本性质biqujian shanglianxuhanshu de jiben xingzhi

❶最大值最小值定理 若函数f (x)在闭区间 [a,b]上连续，则函数f (x)在[a,b]上有最大值与最小值.即存在x₁ ,x₂ ∈〔 [a,b] ，使得对于一切x∈[a,b]，总有f (x₁)≤f(x)≤f (x₂)。
推论 （有界性定理） 若函数f (x)在闭区间[a,b]上连续，则函数f (x)在 [a,b]上有界。

❷介值定理 若函数f (x)在闭区间 [a,b]上连续，且f (a) ≠f (b)，则对于f (a)与f (b)之间的任意一个数c，在 (a,6)内至少存在一点x₀ ，使得f (x₀) =c。

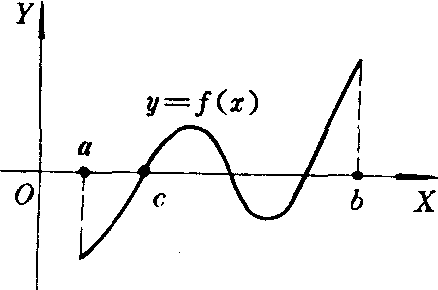
推论1 （根的存在性定理） 若函数f (x)在闭区间[a,b]上连续，且f (a) f (b)<0，则在区间 (a,b) 内至少存在一点c，使得f (c) = 0。
推论2 若函数f (x)在闭區间 [a,b]上连续，则f (x) 的值域为闭区间 [m,M]，其中M,m分别为f (x)在 [a,b]上的最大值和最小值。
以上性质都具有明显的几何意义。如根的存在性定理的几何意义是，若点A (a ,f (a)) 与B (b,f (b))分别在X轴的上下两侧，则连结A,B的连续曲线y=f (x)与X轴至少有一个交点 （如上图）。