邻接矩阵linjie juzhen

能表示图的一种矩阵.设G=〈V,E〉为简单图，V={v₁,v₂，…，v_n}，则n阶方阵

称为G的邻接矩阵.
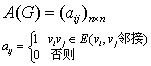
当且仅当图G没有边时，A(G) =0.如图

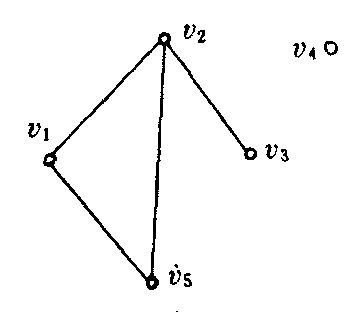
G₁

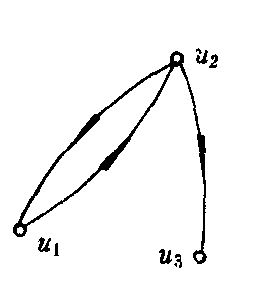
G₂

G₁,G₂的邻接矩阵分别为

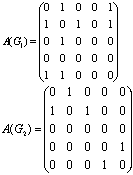
简单无向图的邻接矩阵是对称方阵，主对角线上元素全为0，第i行1的个数恰为v_i的度数.
简单有向图的邻接矩阵未必是对称方阵，主对角线上元素全为0，第i行1的个数是v_i的出度d⁺(v_i)，第j列1的个数是vi的入度d-(vj).
简单图的邻接矩阵描述了图的全部信息.因而可以认为邻接矩阵就是图本身.
将G的点重新编号得图G₁，则G与G₁的邻接矩阵适合以下关系

A (G1)=P^-1A (G) P=P⋅A (G) P

式中P为某n阶置换方阵，即每行每列只有1个1其余均为0的n阶方阵.
G的邻接矩阵A (G)=(a_ij)的元素a_ij可解释为v_i到v_j是否有长为1的路，即a_ij＝1时，v_i,v_j邻接，认为有长为1的路；a_ij＝0,v_i,v_j不邻接，没有长为1的路.
更一般，设G的邻接矩阵为A (G)，则(A (G))^t的第i行第j列元a_ij(l)等于G中v_i到v_j的长为l的路的条数.
例如图

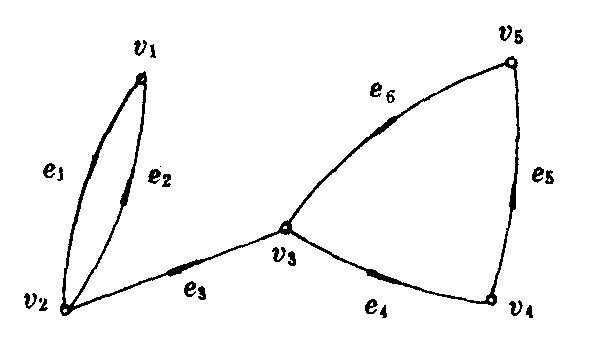
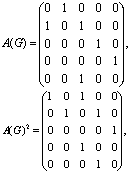
由A (G)²可看出v₁到v₁的长为2的路有1条，即v₁e₁v₂e₂v₁;v₁到v₃长为2的路有1条，即v₁e₁v₂e₃v₃；等等.
利用G= (V,E>,|V|=n，任二点间若有路，必有长≤n-1的路 (若有回路，则有长≤n的回路)，则

B =A(G)+A(G)²十A(G)³ +…+A(G)ⁿ

给出G中任二点 （包括到自身的回路） 间长度小于等于R的路的总条数. B称为G的通路矩阵或路径矩阵.
于是，前面例子中G的通路矩阵为

若将G的通路矩阵B的非0元素换为1,0保持不动，得到矩阵P.则P称为G的可达性矩阵. P刻划了任二点之间是否有路这一重要属性而舍弃了路的长度及条数. 可达性矩阵也可直接定义如下：

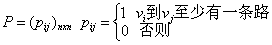
还可用下述方法求P.在计算A (G)。时，将非0元素换为1,0保持不动，得A (G)⁽²⁾; 再利用A (G)(3)=A (G) ·A (G)⁽²) 直接计算A (G) ·A (G)⁽²⁾，且化简得A (G) ⁽³⁾，即将非0元素换为1,0保持不动. 依次可得
A(G)⁽⁴⁾，…，A(G)⁽ⁿ⁾，最后将

A (G) +A (G)⁽²⁾+…+A (G)⁽ⁿ⁾

的非0元素换为1,0保持不动，得到的就是可达性矩阵P.