如果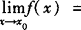 a,
a,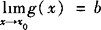 ,那么
,那么
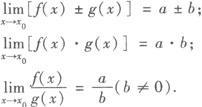
【说明】 在进行函数极限的运算时,还经常用到下面的结论:
(1)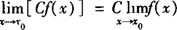 (C是常数);
(C是常数);
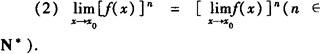
一个重要结论:
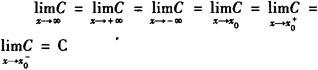
例1 讨论下列函数当x→+∞,x→—∞和x→∞时的极限.
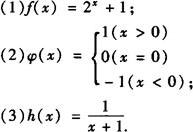
解 根据函数f(x)当x→+∞,x→—∞,x→∞时极限的定义,观察函数值变化的趋势,结合函数图象得出的结论.
(1)由下图可知,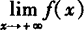 不存在,
不存在,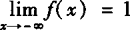 ,
,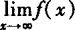 不存在.
不存在.
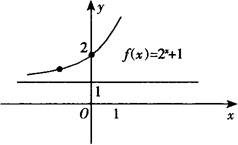
(2)由下图可知,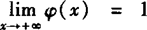 ,
,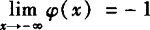 ,
,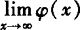 不存在.
不存在.
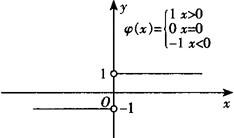
(3)由图可知,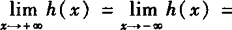 0,∴
0,∴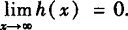 .
.
当a,b取何值时,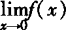 存在,其值为多少?
存在,其值为多少?
解 x=0是此分段函数的分界点,而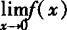 存在的充要条件
存在的充要条件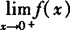 与
与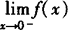 都存在并且相等∴
都存在并且相等∴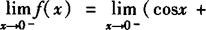
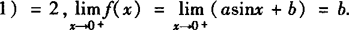 .
.
∴当b=2,a取任意常数时,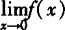 存在,其值为2.
存在,其值为2.
例3 研究函数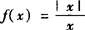 在x=0处的左、右极限.
在x=0处的左、右极限.
解 由于x<0时,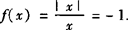 .
.
所以当x→0—时,f(x)→—1,
故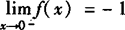
而当x>0时, ,
,
∴当x→0+时,f(x)→1,
因此,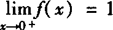 .
.
由于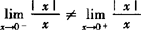
所以 不存在.
不存在.
探索延拓创新
例4 求证: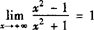 .
.
解 对照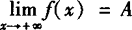 的定义进行证明.
的定义进行证明.
注意到当x>0时,有

- 早慧的儿童是什么意思
- 早慨是什么意思
- 早成是什么意思
- 早成功是什么意思
- 早成者未必有成是什么意思
- 早成者未必有成,晚达者未必不达是什么意思
- 早成雏是什么意思
- 早成鸟是什么意思
- 早成,早熟是什么意思
- 早截是什么意思
- 早户是什么意思
- 早抖是什么意思
- 早报是什么意思
- 早报明年律应,又还依旧先开。是什么意思
- 早拜年是什么意思
- 早挈是什么意思
- 早排是什么意思
- 早接力是什么意思
- 早搏是什么意思
- 早搏后p-r间期延长是什么意思
- 早搏后p波改变是什么意思
- 早搏后qrs波群变化是什么意思
- 早搏后t波改变是什么意思
- 早搏后u波改变是什么意思
- 早搏后同源性逸搏是什么意思
- 早搏后强化是什么意思
- 早搏后心电图改变是什么意思
- 早搏后节律抑制是什么意思
- 早搏后节律提前是什么意思
- 早搏后节律顺延是什么意思
- 早搏后起搏点转移是什么意思
- 早搏后频率加速是什么意思
- 早搏性交界性心动过速是什么意思
- 早搏性室性心动过速是什么意思
- 早搏性心动过速是什么意思
- 早搏性房性心动过速是什么意思
- 早搏性窦性心动过速是什么意思
- 早搏指数是什么意思
- 早搏波形正常化是什么意思
- 早操是什么意思
- 早操和课间操是什么意思
- 早收迟付和早付迟收是什么意思
- 早教是什么意思
- 早教原则是什么意思
- 早断是什么意思
- 早日是什么意思
- 早日头是什么意思
- 早日康复是什么意思
- 早日时是什么意思
- 早日昼儿是什么意思
- 早旦是什么意思
- 早早是什么意思
- 早早介介光是什么意思
- 早早做、阑干遮护。是什么意思
- 早早儿是什么意思
- 早早悟、前途不如意。是什么意思
- 早早晨是什么意思
- 早早(儿)是什么意思
- 早时是什么意思
- 早时间是什么意思