逐步回归分析

逐步回归是多元回归中用以选择自变量的一种常用方法。本条目重点介绍的是一种“向前法”。此法的基本思想是：将自变量逐个地引入方程，引入的条件是该自变量的偏回归平方和在未选入的自变量（未选量）中是最大的，并经F检验是有显著性的。另一方面，每引入一个新变量，要对先前已选入方程的变量（已选量）逐个进行F检验，将偏回归平方和最小且无显著性的变量剔除出方程，直至方程外的自变量不能再引入，方程中的自变量不能再剔除为止。另一种是“向后法”，它的基本思想是：首先建立包括全部自变量的回归方程，然后逐步地剔除变量，先对每一自变量作F(或t)检验，剔除无显著性的变量中偏回归平方和最小的自变量，重新建立方程。接着对方程外的自变量逐个进行F检验，将偏回归平方和最大且有显著性的变量引入方程。重复上述过程，直至方程中的所有自变量都有显著性而方程外的自变量都没有显著性为止(例见条目“多元线性回归”例1、2)。此法在自变量不多，特别是无显著性的自变量不多时可以使用。与一般多元回归相比，用逐步回归法求得的回归方程有如下优点：它所含的自变量个数较少，便于应用；它的剩余标准差也较小，方程的稳定性较好； 由于每步都作检验，因而保证了方程中的所有自变量都是有显著性的。逐步回归分析的主要用途是：
(1)建立一个自变量个数较少的多元线性回归方程。它和一般多元回归方程的用途一样，可用于描述某些因素与某一医学现象间的数量关系，疾病的预测预报，辅助诊断等等。
(2) 因素分析。它有助于从大量因素中把对某一医学现象作用显著的因素或因素组找出来，因此在病因分析、疗效分析中有着广泛的应用。但通常还须兼用“向前法”、“向后法”，并适当多采用几个F检验的界值水准，结合专业分析，从中选定比较正确的结果。
求回归方程的方法步骤如下：
设有含量为n的样本，对每个观察单位观察了m个自变量X_j(j=1,2，…m)和一个应变量Y(可记为X_m+1)，得原始数据如表1。

表1 原始数据格式

观察单位 编 号	变 量
	X1	X2	⋯	Xm	Y=Xm+1
1 2 …	X11 X21 …	X12 X22 …	… … …	X1m X2m …	X1,m+1 X2,m+1 …
n	Xn1	Xn2	…	Xnm	Xn,m+1

1. 先规定一个F^*值，作为引入或剔除自变量时进行F检验的界值。对于给定的显著性水准a来说，每一步作检验时的Fa_(1,n-m′-₁)值是不同的，f但由于样本含量n比引入自变量的个数m′大得多(一般在10倍以上)，所以各步的m′虽然不同，但Fa(1,n-m′-1)值都近似相等。故为方便起见，可取一个定数F*作为F检验的标准。2. 计算每个变量的均数j、离均差平方和(l_ii、l_jj)，每两个变量的离均差积和l_ij，以及相关系数r_ij

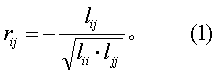
并以求得的_rij为元素列出原始相关矩阵R⁽⁰⁾(阵中r_ij(0)=r_ij):

以后每引入或剔除一个变量都计为一步运算。设R⁽⁰⁾经L步所得的R⁽L⁾为

对于每一步，R(L)均同样按式(2)变换成R(L+1)。设引入或剔除的变量为Xg(g为该变量的下标)，按式(2)作变换Lg，则R^(L)成R^(L+1)时，两矩阵中的各元素rij，有如下关系式：

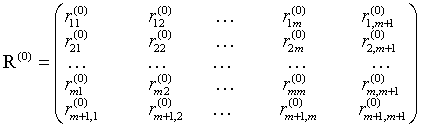
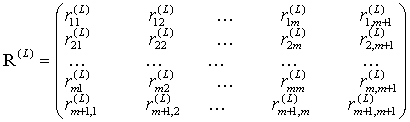
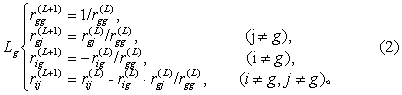
3. 选自变量。
(1) 引入未选量。按式(3)计算各未选量的偏回归平方和V^j(L+1)

找出其中最大者，记作Va^(L+1)，就它所对应的自变量Xa按式(4)作F检验：

式中m′为已引入变量的个数。当F1>F*时引入变量X_a，并对R⁽L⁾按式(2)作变换La，得R⁽L+¹⁾；当F₁≤F^*时挑选变量工作就此结束。
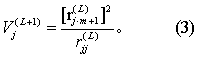
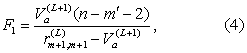
(2)剔除已选量。引入新变量后，对原先引入的已选量分别计算其偏回归平方和Vj(L⁾:

找出V_j(L)中最小者，记作Vb(L)。就Vb(L)所对应的自变量X_b按式(6)作F检验。

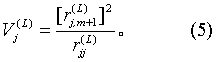
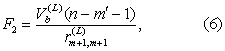
当F₂≤F*时，剔除Xb，并对R(L)按式(2)作变换Lb得R(L+1)；下一步对其余已选量再按式(5)、(6)求Vj并作F检验，直到已选量中没有可剔除时为止；当F₂>F^*时，已选量都不能被剔除，于是再考虑从未选量中能否引入新变量。如此反复进行到第L步，若已选量都不能被剔除，未选量都不能引入时，逐步运算结束。
4. 求回归方程。由相关矩阵R(L)求得的回归方程

称为标准回归方程，式中b′j是标准偏回归系数，按式(7)求得。

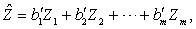
b'j=rj.m+1(L)。(7)

实用中多元线性回归方程常用变量Xj的原单位，因此须再按式(8)求化成原单位后X_j的偏回归系数b_j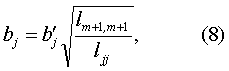

式中l_m+1,m+1＝l_YY，即Y的离均差平方和，l_jj为X_j的离均差平方和。回归方程的常数项按式(9)计算，

b₀＝-∑bjj,(9)

式中j为已选量的下标。于是得多元回归方程为

Ŷ=b₀+∑bjXj。 (10)

5. 回归方程的线性假设检验。按式(11)作方差分析。

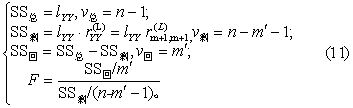
回归的剩余标准差s按式(12)计算。

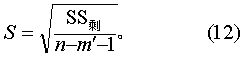
其意义及用途见条目“多元线性回归”。
多元相关系数R按式(13)计算，R的意义、用途及假设检验见条目“多元线性相关”。

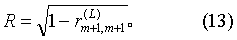
求得多元线性回归方程后，就可利用它来进行预测，参见条目“多元线性回归”。
例 某单位为了研究正常少年儿童的心象面积与性别、月龄、身高、体重、胸围的关系，调查了521名2.5～15岁的正常少儿，资料见表2，试用逐步回归法求预测心象面积的回归方程。

表2 521名正常儿童各项指标的部分记录

编号	性别* X1	月龄 （月） X2	身高 (cm) X3	体重 (kg) X4	胸围 (cm) X5	实测心象面积 (cm2) Y=X6
1 2 3 ⋮	1 1 1 ⋮	32 33 35 ⋮	95.5 92.0 89.0 ⋮	14.0 13.0 12.5 ⋮	53.5 52.0 53.5 ⋮	49.64 41.61 35.81 ⋮
520 521	0 0	176 178	156.0 163.0	55.0 51.0	83.0 79.0	94.60 87.42

*男记作1，女记作0
(1)规定F^*值。本例n=521，估计可能选入4个自变量。对于给定的α=0.05,F₀.₀₅(₁₅₁₆)≐3.86，故取F^*＝3.86。
(2)计算各变量的均数j与离均差平方和l_jj得：

j	1	2	3	4	5	6
j	0.4875	102.37	124.47	24.76	60.23	61.75
ljj	130.17	1016518.26	218849.10	48820.54	29980.76	127402.29

以及离均差积和l_ij（略）。
计算相关系数r_ij,并以r_ij为元素列矩阵R⁽⁰⁾(r_ij(0)=r_ij),

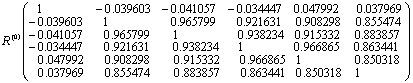
(3)选自变量。
第一步： 选第一个自变量。对全部自变量按式(3)计算V_i(1)得

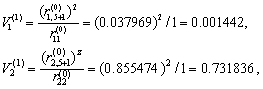
同理，V3(1)=0.781203,V4(1)=0.745530,V5(1)=0.723041。其中V³(1)最大即Vα，按式(4)作F检验。

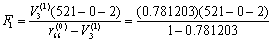＝1853.06>F^*
故引入变量X₃。对R(⁰⁾按式(2)作变换L₂，此时g=3,L=0。

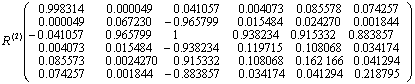
第二步：选第二个自变量。计算各未选量的V_j⁽²⁾:V₁⁽²⁾＝0. 005523,V2(2)=0.000050,V⁽²⁾₄＝0.009755,V⁽²⁾₅＝0.010515，其中V5(2)最大，经F检验有显著性，故引入变量X₅，对R⁽¹⁾仍按式(2)作变换L5，这时g=5,L=1，得R⁽²⁾（略）。
第三步：由于新变量X₅的引入方程，对原有变量X₃应重新检验，为此计算V⁽²⁾₃。按式(5)得

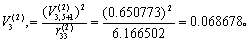
再按式(6)作F检验：

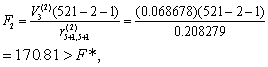
故X₃不能剔除。于是考虑引入第三个自变量，计算各未选量的V_j⁽³⁾:V₁⁽³⁾＝0.002888,V₂⁽³⁾＝0.000295,V₄⁽³⁾＝0.000928，其中V₁⁽³⁾最大，经F检验有显著性，故引入X₁，对R(2)作变换L₁，这时g=1,L=2，得R(3)（略）。
第四步：由于X1的引入，对已选量X3、X₅重作检验。计算得V₃⁽³⁾＝0.071558,V₅⁽³⁾＝0.007880，对其最小者作F检验，得

故原有已选量不能剔除。考虑引入第四个自变量，计算各未选量的V_j⁽⁴⁾: V₂⁽⁴⁾＝0.000208,V₄⁽⁴⁾＝0.002046，其中V₄⁽⁴⁾最大，经F检验有显著性，引入X₄，对R(3)作变换L₄，这时g=4,L=3，得R⁽⁴⁾（略）。
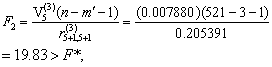
第五步：由于X₄的引入，应对原有的X₁、X₂、X₅重作检验，计算得V₁⁽⁴⁾＝0.004005,V₃⁽⁴⁾＝0.044834,V₅⁽⁴⁾＝0.000341，其中V₅⁽⁴⁾最小。按式(6)作F检验，

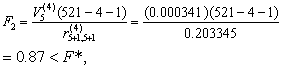
故剔除XS。对R(4)仍按式(2)作变换L5，此时g=5,L=4，得R(5)（略）。
第六步：上步剔除了X₅后，应考虑其余已选量X₁、X₃、X₄还须剔除否。为此计算得V₁⁽⁵⁾ =0.005352,V₃⁽⁵⁾＝0.046192,V₄⁽⁵⁾＝0.009584，其中V₁⁽⁵⁾最小。作F检验，得F₂＝13.59>F*。故已选量都不能剔除。再考虑未选量X₂、X₅能否选入。由于X₅刚被剔除，可不考虑，为此计算V₂⁽⁶⁾＝0.000099，作F检验，得F₁＝0.252。至此，方程外的变量不能进入，方程内的变量不能剔除，逐步运算到此结束。共选进了三个自变量： X₁、X₃、X₄。兹节录R(⁵⁾中的最后一列：

r⁽⁵⁾₁₆＝0.073228,r⁽⁵⁾₂₆＝-0.002541,r⁽⁵⁾₃₆＝0.621366,
r⁽⁵⁾₄₆＝0.282975,r⁽⁵⁾₅₆＝0.004447,r⁽⁵⁾₆₆＝0.203686。

据式(7)及R⁽⁵⁾可得标准偏回归系数为b′1=r⁽⁵⁾₁₆＝0.0732 ,b′3=r⁽⁵⁾₃₆＝0.6214,b′4=r⁽⁵⁾₄₆＝0.2830。
再按式(8)换算成按原单位的偏回归系数，得

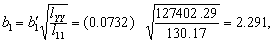
仿此，b3=0.474,b4=0.460。
按式(9),
b₀＝-b₁₁ - b₃₃-b₄₄
＝61.75-2.291 × 0.4875-0.474 × 124.47-0.460 × 24.76 =-9.755。
按式(10)，得回归方程为
Ŷ=-9.755 + 2.291X₁+0.474 X₃ + 0.460X₄
即心象面积(cm)²＝-9.755+2.291性别(男为1，女为0)+0.474身高(cm)+0.460体重(kg)。
对此方程作线性假设检验。列方差分析表(表3)，表中SS、ν、MS及F值均按式(11)求得。查F界值表，得P值，按a=0.05水准，此方程有显著性，即方程有效。

表3 方差分析

变异来源	SS	v	MS	F	P
总	127402.29	520
回归	101452.22	3	33817.41	673.74	<0.01
剩余	25950.06	517	50.19

方程的线性假设检验还可按式(13)求得多元相关系数

查F界值表得P<0.01，结论同上。

逐步回归分析stepwise regression analysis

选择自变量以建立最优回归方程的回归分析方法。最优回归方程，指在回归方程中，包含所有对因变量有显著影响的自变量，而不包含对因变量影响不显著的自变量。过程是： 按自变量对因变量影响效应，由大到小逐个把有显著影响的自变量引入回归方程，而那些对因变量影响不显著的变量则可能被忽略。另外，已被引入回归方程的变量在引入新变量后，其重要性可能会发生变化，当效应不显著时，则需要从回归方程中将此变量剔除。引入一个变量或从回归方程中剔除一个变量都称为逐步回归的一步。每一步都要进行F检验，以保证在引入新变量前回归方程中只含有对因变量影响显著的变量，而不显著的变量已被剔除。直到回归方程中所有变量都不能剔除而又没有新变量可以引入时为止，逐步回归过程结束。实际应用时，需要注重逐步回归分析跟自己研究假设之间的关联。由于运算过程比较复杂，可通过统计软件中的回归分析模块进行。