迪基-富勒(D-F)检验Dickey-Fuller Test

检验经济和金融变量是否是随机游走，这类研究利用了David Dickey和Wayne Fuller的单位根检验。
假定我们相信有增长趋势的变量Y_t可由下式描述

Y_t＝α+βt+ρY_t-1+ε_t (1)

一个可能性是Y_t在不断的增长，因为它有正的趋势(β>0)，但在剔除趋势后，它是平稳的(即|ρ|<1)。在这种情况下，方程(1)的回归有意义。另一种可能性是Y_t在不断增长，因为它是个伴随正位移的随机游走(即α>0,β=0且ρ=1)。这种情况，我们应该对△Y_t进行研究，将Y_t剔除趋势后也不是平稳的，方程(即使Y_t已剔除趋势)也将导致虚假的结果。
有人可能会想方程(1)可由OLS进行估计，关于ρ的t统计量可用于检验ρ是否显著不等于1。然而，如果ρ的真实值为1，则OLS估计是有偏的。这样，以这种方式使用OLS将导致不该拒绝随机游走假设时而拒绝了。
方程(1)的一个问题是它隐含了一个假设，即误差项ε_t不存在序列相关。我们经常在ε_t有序列相关时，也能进行单位根检验。这可由扩展Dickey-Fuller检验实现。这个检验将方程(1)右边扩展为包含Y_t滞后变化量的项：

其中△Y_t＝Y_t-Y_t-1。滞后项个数的选择标准是使误差项ε_t不存在序列相关。
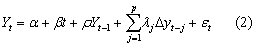
此时的单位根检验步骤如下：首先，对无限制回归方程

应用OLS进行估计。然后，对限制回归方程

应用OLS进行估计。最后，计算出标准F比率用以检验限制(β=0且ρ=1)是否成立。我们必须使用Dickey和Fuller分布表来进行检验。

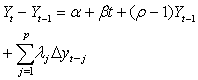
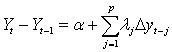
Dickey和Fuller分布表

样本大小	F比率小于临界值的概率
N	0.01	0.025	0.05	0.10	0.90	0.95	0.975	0.99
25	0.74	0.90	1.08	1.33	5.91	7.24	8.65	10.61
50	0.76	0.93	1.11	1.37	5.61	6.73	7.81	9.31
100	0.76	0.94	1.12	1.38	5.47	6.49	7.44	8.73
250	0.76	0.94	1.13	1.39	5.39	6.34	7.25	8.43
500	0.76	0.94	1.13	1.39	5.36	6.30	7.20	8.34
∞	0.77	0.94	1.13	1.39	5.34	6.25	7.16	8.27
标准误差	0.004	0.004	.003	.004	.015	.020	.032	.058

来源：Dickey and Fuller,op.cit.,Table Ⅵ,p.1063,1981.