贝叶斯公式

设(Ω,F,P)为一概率空间，A₁,A₂，…，A_n为样本空间Ω的一个有限剖分，对于任意的i(i=1,2，…，n)，都有P(A_i)>0，则对事件域F中任一事件B，如果P(B)>0，有P(A_iB)=P(BA_i)·P(A_i)P(BA_i)·P(A_i)　(i=1,2，…，n)此式称为贝叶斯公式，式中P(A_iB)为事件B发生条件下事件A_i发生的条件概率。常被应用于测验分数统计中。

贝叶斯公式beiyesi gongshi

若事件组B₁,B₂，………满足：
❶ B_iB_j＝Φ (i≠J);
❷ P (B_i) =1;
❸P (Bi)>0 (i=1,2，………)则对于任意一事件A,P (A) >0，有如下公式

式称为贝叶斯公式。
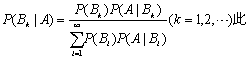
若事件B_i只有n个，公式也成立，此时右端分母只有n项相加。
一般地，把P (B_i|A)称为事后概率 （又称后验概率）,P (B_i)称为事前概率（又称先验概率）。例如，设B₁,B₂，………，B₃是病人可能患的几种不同的疾病，在诊断前先检验与这些疾病有关的某些指标 (如体温、血压，血糖等等)，若病人的某些指标偏离正常值 (即A发生)，要问病人患的是那一种病，从概率论的角度考虑，若P (B_i|A)较大，则病人患B_i种病的可能性也较大。而为了计算P (B_i | A)就可以利用上述的贝叶斯公式，并把由过去的病例中得到的先验概率P (Bi )值代入 (医学上称P(B_i) 为B_i病的发病率)。