菲涅耳直边衍射
菲涅耳直边衍射feinieer zhibian yanshe
障碍物是不透光的直边屏时的菲涅耳衍射。如图1,设S为线状光源,F是直边屏。由屏边一点O对光源作垂线,交屏幕于P0。这就是几何影界。由图形的对称性可知,此时对于P0点可将过O点的柱面波阵面分成以OP0为中线的许多直条形的菲涅耳半波带。利用菲涅耳积分或考纽螺线的计算结果如图2,横坐标正向表示几何影区外距影界的距离;负向表示影区内距影界的距离。纵坐标表示某点光振幅与没有障碍物时振幅之比。由图2可知,对影界上的P0点,振幅降为没有障碍物时的1/2,光强降为1/4。对影区外,将出现明暗交替的条纹,只有在离影界足够远,才有匀光强分布。在几何影区内,光强单调下降直至趋于零。
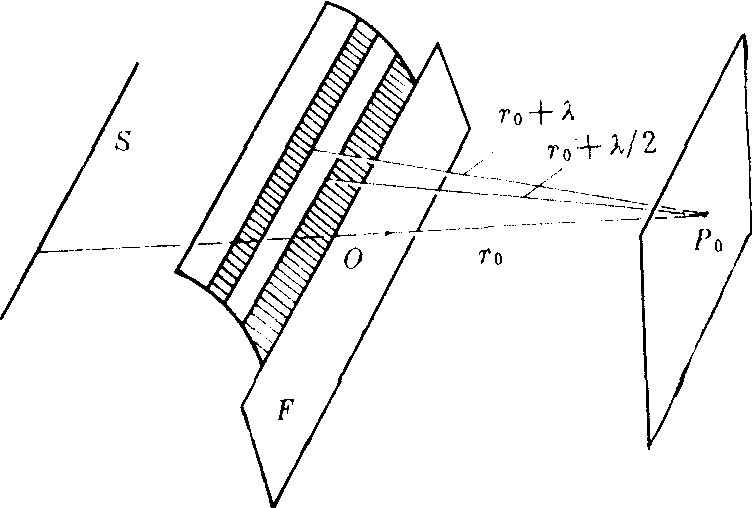
图1
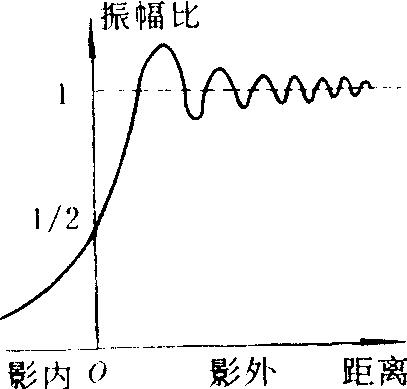
图2
直边衍射是菲涅耳最早研究并解决的光的衍射问题之一,在确立光的波动说方面起过作用。利用菲涅耳直边衍射理论可以解决一些其它衍射问题。如菲涅耳单狭缝衍射,可把狭缝看作两个相距很近的平行直边屏,计算结果与实验符合较好。同样,也可研究以不透明直条代替狭缝而得的菲涅耳单丝衍射。
☚ 泊松点 夫琅和费衍射 ☛
- 事业部门制企业组织结构是什么意思
- 事中是什么意思
- 事中审计是什么意思
- 事中稽核是什么意思
- 事中见指是什么意思
- 事主是什么意思
- 事主及盗私相休和是什么意思
- 事主家是什么意思
- 事主杀死盗是什么意思
- 事久多变,礼繁则乱是什么意思
- 事久多变,萧坦之先下手是什么意思
- 事久见人心是什么意思
- 事义是什么意思
- 事之宣泄,受罪不测是什么意思
- 事之成败,必由小生是什么意思
- 事之成败,必由小生。是什么意思
- 事之至近而所系至大者,莫过于言语饮食也。是什么意思
- 事之至难,莫如知人;事之至大,亦莫如知人是什么意思
- 事之行也有势,其成也有气。是什么意思
- 事之难易,不在小大,务在知时是什么意思
- 事事是什么意思
- 事事儿是什么意思
- 事事关心是什么意思
- 事事只在道理上商量,便是真体认。是什么意思
- 事事如意是什么意思
- 事事得心应手,都能取得好的效果是什么意思
- 事事无成是什么意思
- 事事有实际,言言有妙境,物物有至理,人人有处法,所贵乎学者学此而已。无地而不学,无时而不学,无念而不学,不会其全,不诣其极不止,此之谓学者。今之学者果如是乎?留心于浩瀚博杂之书,役志于靡丽刻削之辞,耽心于凿真乱俗之技,争胜于烦劳苛琐之仪,可哀矣。而醉梦者又贸贸昏昏,若痴是什么意思
- 事事棘手是什么意思
- 事事物物是什么意思
- 事事皆有规律是什么意思
- 事事笨拙是什么意思
- 事事躬亲是什么意思
- 事事都吉利是什么意思
- 事亡如存是什么意思
- 事亲不欺是什么意思
- 事亲为大,守身为大是什么意思
- 事亲以得欢心为本是什么意思
- 事亲孝,故忠可移于君是什么意思
- 事亲守身是什么意思
- 事人是什么意思
- 事从两来,莫怪一人是什么意思
- 事从容则有余味,人从容则有余年是什么意思
- 事从根起,藕发莲生是什么意思
- 事从缓来是什么意思
- 事从缓来。是什么意思
- 事从脚跟起是什么意思
- 事仔是什么意思
- 事以密成是什么意思
- 事以密成,语以泄败是什么意思
- 事以密成,语以泄败。是什么意思
- 事以微巧成,以疏拙政是什么意思
- 事以急而败者,十之七八是什么意思
- 事以急而败者,十常七八是什么意思
- 事以急而败者,十常八九是什么意思
- 事以简为上,言以简为当是什么意思
- 事以简为止, 言以简为当。是什么意思
- 事件是什么意思
- 事件·制度·法规是什么意思
- 事件·制度·法规▷是什么意思