奇点理论中十分活跃的研究专题,描述微分流形之间的光滑映射在一点附近最重要的局部性态。
刻划有限决定的映射芽的本质特征,判定一个映射芽在什么条件下有限决定并对其决定性阶数进行估计,是映射芽的决定性理论的基本问题。在1968~1971年期间,马瑟(J.N.Mather)以《C∞映射的稳定性》为总标题发表的6篇系列论文为这一研究奠定了基础。
一般地,在C∞映射芽集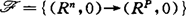 上给定一等价关系,可考虑
上给定一等价关系,可考虑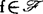 由它的r次导网jrf有限决定的问题。
由它的r次导网jrf有限决定的问题。
马瑟引入了5类C∞微分同胚芽群,并通过这些群在集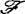 上的作用来规定等价关系,这5类群通常记为
上的作用来规定等价关系,这5类群通常记为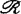 ,
,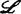 ,
,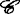 ,
,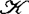 ,
,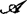 。
。
例如群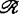 与
与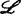 分别由源空间(Rn,0)及靶空间(Rp,0)上的C∞坐标变换组成,
分别由源空间(Rn,0)及靶空间(Rp,0)上的C∞坐标变换组成,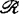 (及
(及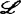 )在
)在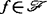 上的作用是通过映射芽复合从右边(及左边)作用在f上。群
上的作用是通过映射芽复合从右边(及左边)作用在f上。群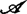 定义为
定义为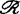 与
与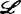 的直积。
的直积。
C∞芽f:(Rn,0)→(Rp,0)是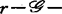 决定的(其中
决定的(其中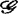 可为上述5类群中的任何一个),是指
可为上述5类群中的任何一个),是指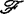 中所有与f具有相同r-导网的映射芽均位于轨道
中所有与f具有相同r-导网的映射芽均位于轨道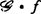 中。而f的
中。而f的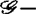 决定性阶数是使得f为
决定性阶数是使得f为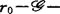 决定的最小正整数r0。例如若f:(Rn,0)→R是莫尔斯函数芽(此时Df(0)=0,且矩阵
决定的最小正整数r0。例如若f:(Rn,0)→R是莫尔斯函数芽(此时Df(0)=0,且矩阵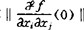 满秩),则由莫尔斯引理知f恰为2-R-决定的。对于一般的
满秩),则由莫尔斯引理知f恰为2-R-决定的。对于一般的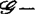 有限决定的C∞芽,在
有限决定的C∞芽,在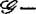 等价意义下,可由它的有限次泰勒展式来完全确定,因而在局部分析中具有重要意义。
等价意义下,可由它的有限次泰勒展式来完全确定,因而在局部分析中具有重要意义。
为叙述马瑟的著名结果,记C∞函数芽环Cn={(Rn,0)→R}的极大理想为mn,令θf表示沿f的C∞向量场芽所组成的Cn模,简记θ1|Rn,0)为θn。tf:θn→θf和ωf:θp→θf分别由tf(ξ)=Tfoξ和ωf(η)=ηof给出。
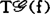 视
视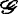 的不同情形分别取为
的不同情形分别取为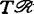 (f)=tf(mnθn),
(f)=tf(mnθn),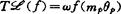 ,
,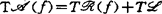 (f),
(f),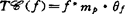 ,
,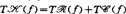 。整数d
。整数d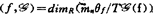 叫做f关于
叫做f关于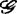 的余维。
的余维。
加夫尼(T.Gaffney)于1979年给出了著名的马瑟无穷小判别法的一个改进形式。
设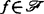 ,则下列各条等价:
,则下列各条等价:
(b)f是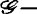 有限决定的,
有限决定的,
(t)对于某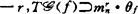 ,
,
(d)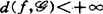 。
。
更精确地,有(i)若f是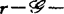 决定的,则
决定的,则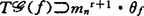 ,(ii)若
,(ii)若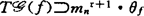 ,则f是
,则f是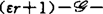 决定,(iii)若d
决定,(iii)若d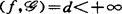 ,则
,则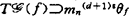 ,其中当
,其中当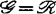 ,
,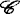 或
或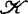 时,ε=1;当
时,ε=1;当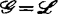 或
或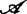 时,ε=2。
时,ε=2。
群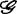 中的成员取s-导网为恒同映射者所成之集
中的成员取s-导网为恒同映射者所成之集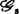 是群
是群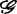 的正规子群,
的正规子群,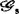 在C∞芽集
在C∞芽集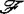 上的作用可定义
上的作用可定义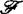 上的等价关系,从而可定义
上的等价关系,从而可定义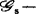 决定性。
决定性。
对于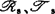 及
及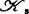 有限决定性,库哈兹(W.Kucharz)于1976年就函数芽、热尔韦(J.-J.Gervais)于1977年就一般的映射芽给出了刻划。1984年布鲁斯(J.W.Bruce)等对
有限决定性,库哈兹(W.Kucharz)于1976年就函数芽、热尔韦(J.-J.Gervais)于1977年就一般的映射芽给出了刻划。1984年布鲁斯(J.W.Bruce)等对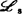 及
及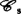 有限决定性提供了另一种形式的刻划,戴蒙(J.Damon)分别对
有限决定性提供了另一种形式的刻划,戴蒙(J.Damon)分别对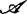 和
和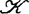 的一类几何子群刻划了有限决定性。
的一类几何子群刻划了有限决定性。
对有限决定性的刻划还可用托姆(R.Thom)提出的通用开折概念来描述,即C∞芽f是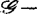 有限决定的,当且仅当f有一个
有限决定的,当且仅当f有一个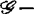 通用开折。通用开折是奇点理论对现代数学最重要的贡献之一,它是突变理论的核心。
通用开折。通用开折是奇点理论对现代数学最重要的贡献之一,它是突变理论的核心。
对应于上述5类群的5种决定性,它们之间具有某种联系,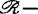 (及
(及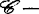 )有限决定性与
)有限决定性与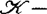 有限决定性相关,
有限决定性相关,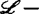 有限决定性与
有限决定性与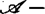 有限决定性又彼此相联。例如若C∞芽
有限决定性又彼此相联。例如若C∞芽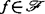 不是浸入与浸没,则f是
不是浸入与浸没,则f是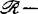 有限决定的
有限决定的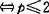 且f是
且f是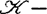 有限决定的。
有限决定的。
假若f是实解析芽,那么f作为C∞芽是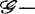 有限决定
有限决定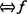 作为实解析芽是
作为实解析芽是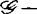 有限决定
有限决定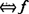 的复化作为全纯芽是y一有限决定。因此在对C∞芽的决定性阶数进行估计时,近十多年来人们的兴趣更多地是就
的复化作为全纯芽是y一有限决定。因此在对C∞芽的决定性阶数进行估计时,近十多年来人们的兴趣更多地是就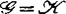 及
及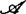 的情形来进行研究。从历史上看,马瑟的工作著重于C∞稳定性、稳定映射的稠密性与分类问题。他对稳定的映射芽的决定性阶数已作出好的估计,并且给出了各类稳定映射芽的标准型,但对非稳定的有限决定的映射芽的阶数估计以及标准型问题尚未深入考虑。
的情形来进行研究。从历史上看,马瑟的工作著重于C∞稳定性、稳定映射的稠密性与分类问题。他对稳定的映射芽的决定性阶数已作出好的估计,并且给出了各类稳定映射芽的标准型,但对非稳定的有限决定的映射芽的阶数估计以及标准型问题尚未深入考虑。
自1975年以来,加夫尼、马蒂内(J.Martinet)以及迪普莱西(A.du Plessis)等提供了一系列好方法用以精确估计决定性阶数。现举下例加以简单说明:设映射芽f:R2,0)→(R2,0),(x,y)→(x,y3+x2y),按照马瑟的估计,f是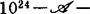 决定的;而依加夫尼的方法,f是
决定的;而依加夫尼的方法,f是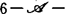 决定的;依迪普莱西的方法则为
决定的;依迪普莱西的方法则为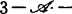 决定的。1985年以来,中国奇点理论工作者在李培信主持下开展了这方面的研究,对
决定的。1985年以来,中国奇点理论工作者在李培信主持下开展了这方面的研究,对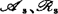 及
及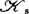 决定性阶数估计取得一些好结果。
决定性阶数估计取得一些好结果。
1979年,布罗德森(H.Brodersen)及威尔逊(L.C.Wilson)同时研究了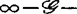 决定性。映射芽
决定性。映射芽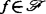 是
是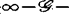 决定的,意指
决定的,意指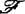 中与f具有相同无穷泰勒级数的每一芽g(此时j∞g(0)=j∞f(0))必
中与f具有相同无穷泰勒级数的每一芽g(此时j∞g(0)=j∞f(0))必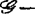 等价于f。此外,在这之前还引入了
等价于f。此外,在这之前还引入了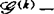 等价性,0≤k<∞。事实上,群
等价性,0≤k<∞。事实上,群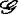 中的成员均为C∞微分同胚芽,若将C∞条件减弱为Ck,即用Ck微分同胚芽来代替便可得到群
中的成员均为C∞微分同胚芽,若将C∞条件减弱为Ck,即用Ck微分同胚芽来代替便可得到群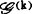 ,由此可诱导出C∞芽集
,由此可诱导出C∞芽集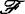 上的等价关系,并且这些等价关系产生相应的
上的等价关系,并且这些等价关系产生相应的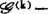 决定性,于是可引入如下一些条件:对任意
决定性,于是可引入如下一些条件:对任意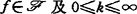 ,
,
(ak)f是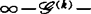 决定的,
决定的,
(bk)f是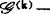 有限决定的,
有限决定的,
(t)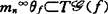 ,
,
(g)存在Rn中原点0的一邻域U及芽f的一个代表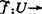 Rp,使得对U-{0}中的每一有限子集S,
Rp,使得对U-{0}中的每一有限子集S,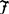 在S处的多重芽是
在S处的多重芽是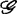 -稳定的。
-稳定的。
几何条件(g)适用于解析芽,为此又引进了条件(e),称为“椭圆性”条件。
例如当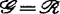 ,
,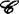 或
或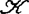 时,取Cn中的理想
时,取Cn中的理想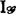 (f)分别为Jf(由Df的p×p子式所生成)、f*mp.Cn及Jf+f*mp·Cn,并且条件(e)要求有限生成的理想
(f)分别为Jf(由Df的p×p子式所生成)、f*mp.Cn及Jf+f*mp·Cn,并且条件(e)要求有限生成的理想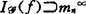 。当然还可以用一组Lojasiewicz不等式来表达条件(e)。
。当然还可以用一组Lojasiewicz不等式来表达条件(e)。
沃尔(C.T.C.Wall)在1981年发表的综述性论文中,将许多学者的研究概括为下述结论:对于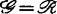 ,
,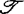 ,
,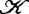 或
或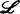 ,下列条件
,下列条件
(ak)(o≤k≤∞),(bk)(0≤k<∞),(t)及(e)是等价的。如果f是解析芽,则上述诸条件还等价于(g)。
而对于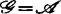 ,布罗德森于1990年在一次奇点理论学术会上报告了下述结果:记条件
,布罗德森于1990年在一次奇点理论学术会上报告了下述结果:记条件
(g′)对于每一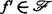 ,若j∞f(0)=j∞f(0),则f′满足(g),
,若j∞f(0)=j∞f(0),则f′满足(g),
又0<k≤∞,则条件(e),(t),(g′)及(a∞)是等价的,并且它们中的每一个与(ak)(p+1≤k<∞)及(bk)(p+1≤k<∞)中的任何一个等价。
在探讨有限决定映射芽的标准型时,自然提出如何识别属于同一等价类中的诸映射芽的问题。
对此问题的研究,导致迪普莱西于1980年引入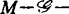 决定性,其中M为(Cn)p的一个Cn-模,现就M=(I)p(I为Cn中理想)简述之。f叫做
决定性,其中M为(Cn)p的一个Cn-模,现就M=(I)p(I为Cn中理想)简述之。f叫做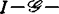 决定,如果g是f的任意一个I-逼近(即要求yjog-yiof∈I,i=1,…,p),则g与f是
决定,如果g是f的任意一个I-逼近(即要求yjog-yiof∈I,i=1,…,p),则g与f是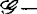 等价的。
等价的。
通常所说的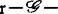 决定性就是这里的
决定性就是这里的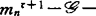 决定性,并且
决定性,并且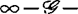 决定性就是
决定性就是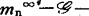 决定性。1982年,加夫尼和迪普莱西对情形
决定性。1982年,加夫尼和迪普莱西对情形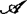 给出如下基本估计:若
给出如下基本估计:若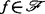 是有限奇异型的,又Cn中理想I满足
是有限奇异型的,又Cn中理想I满足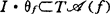 ,则f是
,则f是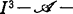 决定的。近几年来,中国一些学者开展了
决定的。近几年来,中国一些学者开展了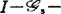 决定性的研究,其中
决定性的研究,其中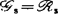 ,
,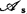 或
或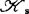 。
。
映射芽的决定性理论还包括不变量的研究(映射芽的余维便是其中之一),以及探讨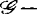 (及
(及 )决定的映射芽是否有普遍意义的问题。
)决定的映射芽是否有普遍意义的问题。
此外,由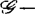 有限决定性进而研究
有限决定性进而研究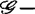 半有限决定性,并且群
半有限决定性,并且群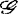 不只限于前述的5类,这说明研究内容十分丰富。由于所讨论的映射芽的定义域是有限维空间,自然会问:能否将所述的理论推广到无穷维情形呢?马格努斯(R.J.Magnus)于1976年曾著文考察过定义在Banach空间上的函数芽的决定性及开折,但至今为止,对于无穷维情形的研究成果似乎不多,有待继续深入。
不只限于前述的5类,这说明研究内容十分丰富。由于所讨论的映射芽的定义域是有限维空间,自然会问:能否将所述的理论推广到无穷维情形呢?马格努斯(R.J.Magnus)于1976年曾著文考察过定义在Banach空间上的函数芽的决定性及开折,但至今为止,对于无穷维情形的研究成果似乎不多,有待继续深入。
1 Mather J N.
I Ann of Math,1968,87:89~104
Ⅱ Annof Math,1969,89:254~291 Ⅲ IHES, 1969,35:127~156 Ⅳ IHES, 1970,37:223~248
V Adv in Math,1970,4:301~336
VI Lecture Notes in Math, 1971,192:207~253
2 du Plessis A. Invent. Math,1980,58:107~160
3 Wall C T C. Bull London Math Soc, 1981,13:481~ 539
4 Gaffney T, et al. Invent Math,1982,66:137~163
5 Damon J. Memoirs Amer Math Soc,1984,50(306)
(湖南师范大学李养成教授撰)
- 秋日明洁的天空是什么意思
- 秋日杂咏是什么意思
- 秋日杂感(二首) - 陈子龙是什么意思
- 秋日杂感(十首选一)是什么意思
- 秋日杂感(选一)是什么意思
- 秋日枯萎的叶是什么意思
- 秋日歌唱是什么意思
- 秋日武关道中是什么意思
- 秋日气候清爽是什么意思
- 秋日泄痢是什么意思
- 秋日泛舟泉湖作 (清)左宗棠是什么意思
- 秋日游昆明池是什么意思
- 秋日游黔灵山途次口占是什么意思
- 秋日湖上是什么意思
- 秋日熟透泛红的果实是什么意思
- 秋日田园杂兴(其八) - 宋·范成大是什么意思
- 秋日田父辞是什么意思
- 秋日登吴公台上寺远眺是什么意思
- 秋日登吴公台上寺远眺寺即陈将吴明彻战场是什么意思
- 秋日登岳阳楼晴望是什么意思
- 秋日登洪府滕王阁饯别序是什么意思
- 秋日登洪府腾王阁饯别序是什么意思
- 秋日登清凉台是什么意思
- 秋日登西城望终南诸峰 (明)康万民是什么意思
- 秋日的云是什么意思
- 秋日的傍晚是什么意思
- 秋日的农事是什么意思
- 秋日的原野是什么意思
- 秋日的叶是什么意思
- 秋日的宴饮是什么意思
- 秋日的山峦是什么意思
- 秋日的心绪是什么意思
- 秋日的思绪情怀是什么意思
- 秋日的悲怨是什么意思
- 秋日的情怀和兴会是什么意思
- 秋日的旅程是什么意思
- 秋日的昏暗景象是什么意思
- 秋日的景色是什么意思
- 秋日的月是什么意思
- 秋日的水波是什么意思
- 秋日的水滨是什么意思
- 秋日的泉水是什么意思
- 秋日的淫雨是什么意思
- 秋日的溪水是什么意思
- 秋日的烟霭是什么意思
- 秋日的眼泪是什么意思
- 秋日的蝉是什么意思
- 秋日的郊野是什么意思
- 秋日的阳光是什么意思
- 秋日的雁是什么意思
- 秋日的霜是什么意思
- 秋日碧澄的天空是什么意思
- 秋日胜春朝是什么意思
- 秋日腌制的菜是什么意思
- 秋日舟中题胡彭举秋江卷是什么意思
- 秋日节日风俗典故是什么意思
- 秋日草木凋零是什么意思
- 秋日荒凉的小路是什么意思
- 秋日行村路是什么意思
- 秋日行村路(乐雷发)是什么意思