11.2.1 傅立叶积分的几种形式
设函数f(x)在无穷区间(-∞,+∞)上绝对可积,定义f(x)的傅立叶积分为
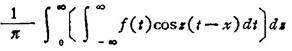
若f(x)的傅立叶积分满足收敛的条件,则傅立叶积分有以下几种形式:
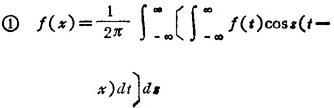
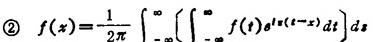
❸ 若f(x)是偶函数,则
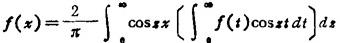
❹ 若f(x)是奇函数,则
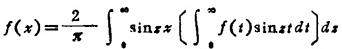
11.2.2 傅立叶变换
定义:设函数f(x)满足
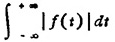
存在:f(x)在(-∞,∞)上满足狄利克莱条件即f(x)只有有限个极值点,只有有限个第一类间断点,则存在
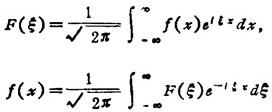
称F(ξ)为f(x)的傅立叶变换,第二式称为傅立叶变换的反演公式。
傅立叶变换的性质:设f(x),g(x)的傅立叶变换分别是F(ξ),G(ξ),则
线性 af(x)+bg(x)的傅立叶变换是aF(ξ)+bG(ξ)。
卷积 f(x)*g(x)=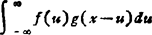 的 傅立叶变换是F(ξ)·G(ξ)。
的 傅立叶变换是F(ξ)·G(ξ)。
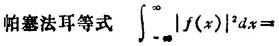
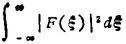
翻转 f(-x)的傅立叶变换是F(-ξ)。
共轭 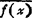 的傅立叶变换是
的傅立叶变换是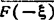 。
。
时移(延迟) f(x-x0)的傅立叶变换是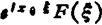 。
。
频移(调频) F(ξ-ξ0)是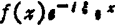 的傅立叶变换(ξ0是常数)。
的傅立叶变换(ξ0是常数)。
11.2.3 傅立叶变换表
见表1.1-16。
表1.1-16 傅立叶变换表

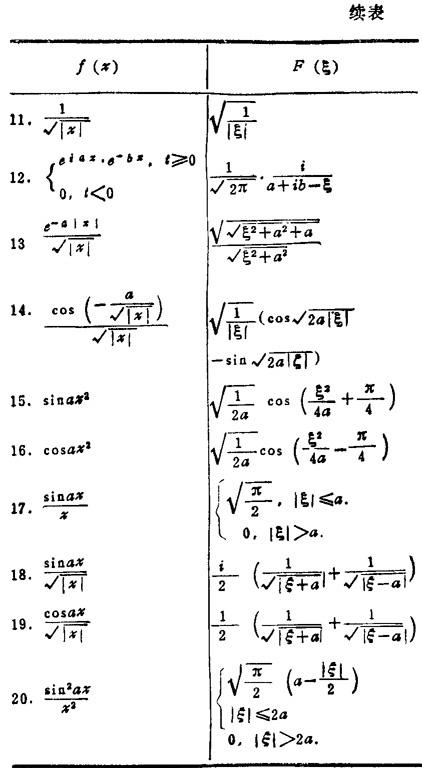
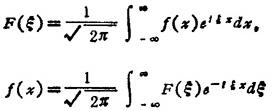
- 四更是什么意思
- 四更·黎简是什么意思
- 四更四鼓是什么意思
- 四更安乐,万事都无想。是什么意思
- 四更山吐月,残夜月明楼。是什么意思
- 四更山吐月,残夜水明楼是什么意思
- 四更山吐月,残夜水明楼.是什么意思
- 四更山吐月,残夜水明楼.尘匣元开镜,风帘自上钩.兔应疑鹤发,蟾亦恋貂裘是什么意思
- 四更水白先疑晓,二月山寒未受春。是什么意思
- 四更里,无事好把真经看。是什么意思
- 四書大全是什么意思
- 四書文是什么意思
- 四書章句集注是什么意思
- 四書院是什么意思
- 四曹是什么意思
- 四最是什么意思
- 四月是什么意思
- 四月二十三日晚同太冲、表之、公实野步 - 宋·洪炎是什么意思
- 四月二十五日致贾平凹书是什么意思
- 四月交响曲是什么意思
- 四月会是什么意思
- 四月兔日祭娅拜是什么意思
- 四月八是什么意思
- 四月八日雨,鱼儿岸下死;四月八日晴,鱼儿上蒿林是什么意思
- 四月八牛王节是什么意思
- 四月八节是什么意思
- 四月八, 冻杀鸭。是什么意思
- 四月初一见青天,高山平地任开田;四月初一满天涂,丢了高田去种湖是什么意思
- 四月初八是什么意思
- 四月初八晴料峭,高田好张钓;四月初八晴寡寡,鲇鱼倒灶下;四月初八乌漉秃,不论上下一齐熟是什么意思
- 四月初八牛生日是什么意思
- 四月初八的来历是什么意思
- 四月十九日泛浣花溪是什么意思
- 四月南风吹百草,一湖晴涨绕千家。是什么意思
- 四月南风大麦黄,枣花未落桐叶长。是什么意思
- 四月南风大麦黄,枣花未落桐阴长是什么意思
- 四月大会是什么意思
- 四月大庙会是什么意思
- 四月天,人换单是什么意思
- 四月子是什么意思
- 四月慢白菜是什么意思
- 四月提纲是什么意思
- 四月文艺社是什么意思
- 四月斋会是什么意思
- 四月梵是什么意思
- 四月的果园——有桃有李是什么意思
- 四月的紫堇花是什么意思
- 四月的青蛙——还能叫一阵子是什么意思
- 四月眉子是什么意思
- 四月荚是什么意思
- 四月豆是什么意思
- 四月豆儿是什么意思
- 四月贡是什么意思
- 四月间晚上的蛤蟆——叫个不停是什么意思
- 四月间的果园是什么意思
- 四月间的桃花是什么意思
- 四月青年是什么意思
- 四月麦秀寒,五月温和暖是什么意思
- 四有是什么意思
- 四有三讲两不怕是什么意思