罗伊恒等式Roy's Identity
在消费者理论中,设价格p=(p1,…,pn)>0, 收入为w。当间接效用函数ν(p,w)可微时, 对p=(p1,…,pn)>0和w>0,有xi(p,w)=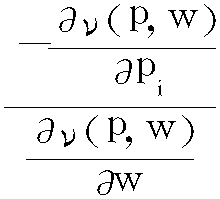 ,i=1,2,…,n。其中,xi(p,w)是在价格p和收入w之下消费者对第i种商品的需求函数,称为罗伊恒等式。
,i=1,2,…,n。其中,xi(p,w)是在价格p和收入w之下消费者对第i种商品的需求函数,称为罗伊恒等式。
罗伊恒等式
罗伊恒等式Roy’s Identity
在消费者理论中,设价格p=(p1,…,pn),收入为w。当间接效用函数v(p,w)是可微时,对p=(p1,…,pn)>0和w>0,有
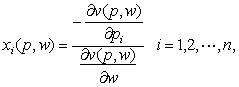
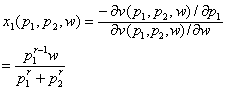
☚ 间接效用函数 补偿需求函数 ☛
- 法国动物运输管理立法是什么意思
- 法国动物饲养治理立法是什么意思
- 法国十九世纪农村风景画是什么意思
- 法国华侨协会是什么意思
- 法国华裔互助会是什么意思
- 法国华裔社会福利敬老中心是什么意思
- 法国南大门是什么意思
- 法国博物馆日是什么意思
- 法国占领鲁尔事件是什么意思
- 法国危险动物管理立法是什么意思
- 法国历届总统小史是什么意思
- 法国参议院是什么意思
- 法国友丰书店是什么意思
- 法国古典建筑是什么意思
- 法国古典管理理论是什么意思
- 法国史是什么意思
- 法国史学对史学理论的贡献是什么意思
- 法国司法警察总局是什么意思
- 法国合作信贷组织是什么意思
- 法国合作社任务立法是什么意思
- 法国合作社储备立法是什么意思
- 法国合作社分配立法是什么意思
- 法国合作社处罚立法是什么意思
- 法国合作社监督立法是什么意思
- 法国合作社管理立法是什么意思
- 法国合作社股份立法是什么意思
- 法国合作金融组织是什么意思
- 法国合同法是什么意思
- 法国名诗人抒情诗选是什么意思
- 法国启蒙运动是什么意思
- 法国品种种子鉴定立法是什么意思
- 法国商业银行是什么意思
- 法国商业银行体制是什么意思
- 法国商堡府邸是什么意思
- 法国商标法是什么意思
- 法国商标法是什么意思
- 法国商法典是什么意思
- 法国四十年的土地政策是什么意思
- 法国国土整治与区域发展政策是什么意思
- 法国国家信贷委员会是什么意思
- 法国国家信贷银行是什么意思
- 法国国家公园分类管理立法是什么意思
- 法国国家公园管理机构立法是什么意思
- 法国国家农业信贷管理局是什么意思
- 法国国家图书馆是什么意思
- 法国国家巴黎银行是什么意思
- 法国国家市场金库是什么意思
- 法国国家林业机构立法是什么意思
- 法国国家管弦乐团是什么意思
- 法国国家行政法院是什么意思
- 法国国有化经济是什么意思
- 法国国有化运动是什么意思
- 法国国民林业基金立法是什么意思
- 法国国民议会是什么意思
- 法国国立农业研究院是什么意思
- 法国国际收支平衡表的编制方法是什么意思
- 法国图书与阅读月是什么意思
- 法国图书节是什么意思
- 法国土地信贷银行是什么意思
- 法国土地整治和农村安置公司是什么意思