组织的超声鉴别

超声波在生物组织内传播时与生物介质相互作用，利用组织对超声波的响应可以从超声信号中获取组织结构的信息。所谓生物组织的超声鉴别就是通过测量组织的超声参数间接地估测组织结构的物理学参数，如组织的密度、排列方向、内部及表面结构及其与病理变化的联系等。上述超声参数包括超声在组织中的传播速度、介质对超声的衰减与吸收、声阻抗、散射能量的频率分布（频谱）及散射角。
纵声波在理想的线性弹性均匀介质中的传播速度为：
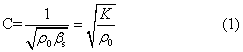　式中ρ0为介质的平均密度，βs为绝热压缩系数，它是绝热体积弹性模量K的倒数。
动物软组织的超声传播速度与稀盐溶液的速度值十分接近。各种软组织的声速差别甚小，只有脂肪组织例外。脂肪组织中的声速比非脂肪软组织约低10%。肺组织中的声速在低频区近似地随频率的升高而线性地增加，但其速度值显著低于其它软组织且与充气状况有关。
人颅骨样品中的声速几乎是软组织声速的两倍。

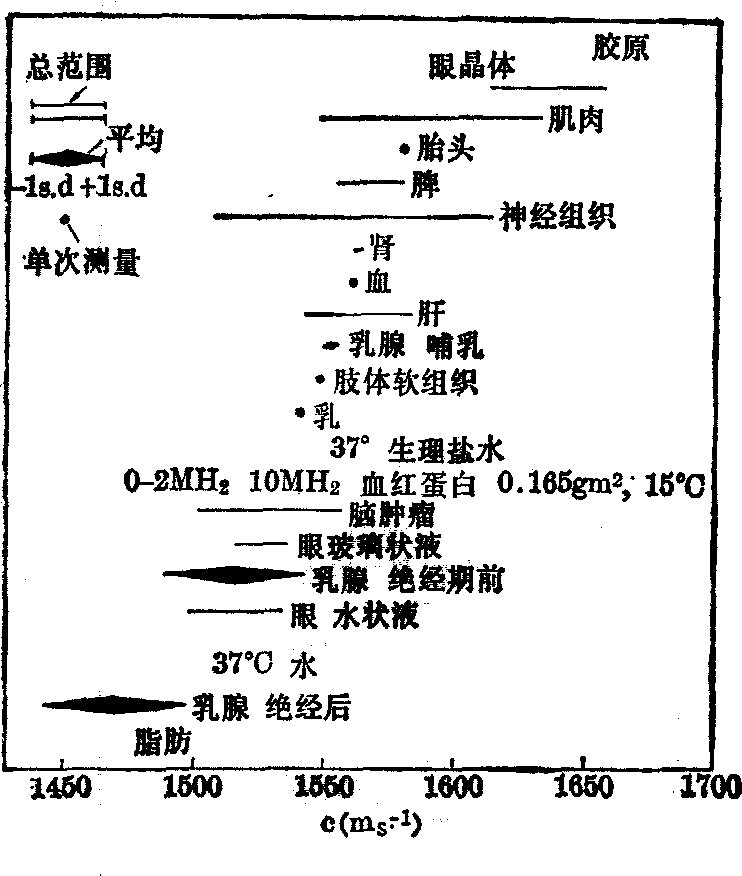
图1 组织的超声传播速度

生物组织中的超声传播速度如图(1)所示。
声场中某位置的声压p为
p=P-P₀ (2)式中P为声场中某一点的瞬时压强，P₀为介质的恒定平衡压强。
声场中某位置的声压p与该位置的质点速度v的比值被定义为该位置的声阻抗率zs,
zs=p/v (3)声阻抗率zs一般可能是复数，在理想媒质中声阻抗率的实数部分反映了能量从一处向另一处的转移 （传播损耗）。在平面声场中各位置上的声阻抗率数值上都相同，且为一实数ρ₀c。这反映了在平面声场各位置上都没有能量的贮存，前一个位置上的能量可以完全被传播到后面的位置上去。乘积ρ0c值是介质固有的一个常数，它称为介质的特性阻抗，记为R。

软组织的密度、弹性性质和声速都与水十分相近。所以可以采用处理液体的方法近似地处理软组织。
各种生物组织的密度和特性阻抗的数值并不相同 (表1)
一列平面波从一媒质垂直投射到媒质的分界面上，由于分界面二边媒质的特性阻抗不一样，一般就会有一部分声波被反射回去，另一部分透入界面另一边的媒质中去。在分界面上反射波声压与入射波声压之比rp，反射波质点速度与入射波质点速度之比rv，透射波声压与入射波声压之比tp以及透射波质点速度与入射波质点速度之比tv分别为

别代表界面二侧的介质。所以声波在分界面上反射与透

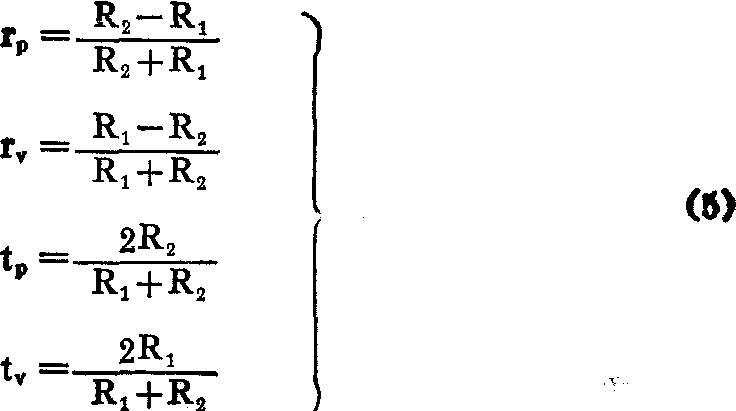
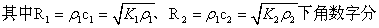
表1 生物组织的密度和特性阻抗

材料	密度g/ml	特性阻抗×106kg/m2s
血液 骨 脑 脂肪 肾 肝 肌肉 脾 水 肺	1.06 1.38～1.81 1.03 0.92 1.04 1.06 1.07 1.06 1.00 0.40	1.62 3.75～7.38 1.55～1.66 1.35 1.62 1.64～1.68 1.65～1.74 1.65～1.67 1.52 0.26

射的大小仅取决于媒质的特性阻抗。

表2是一些生物组织界面的反射率的数值。表2 一些生物组织界面的反射率(以低于全反射器反射率的分贝数表示，注*的界面无实际意义)

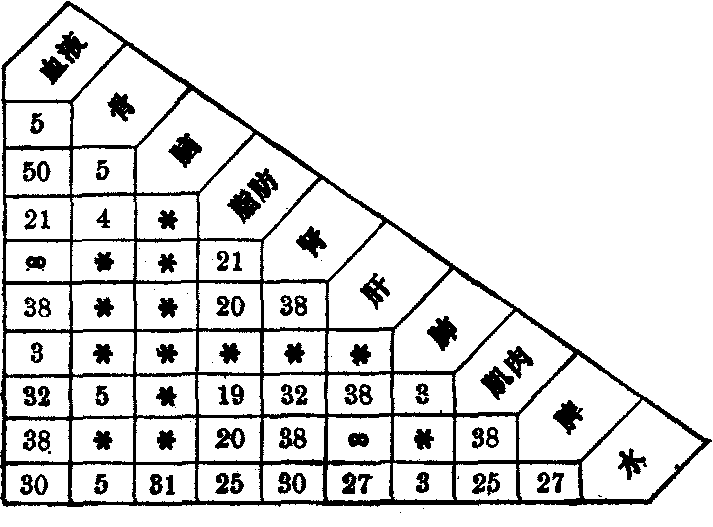
对于各种声学测量来说衰减系数α和超声传播速度c是二个基本物理量。超声波通过真实介质时它的强度是传播距离的函数，随着传播距离增大，强度亦随之下降。造成这种衰减现象的因素有：
❶波束扩展导致单位面积的能量下降。
❷散射作用使一部分能量偏离原来的传播方向。
❸波的模式改变，导致能量在具有不同波速和不同传播方向的波之间进行重新分配。
❹吸收过程，超声能量转变为热。在具有衰减作用的真实介质中一列沿x方向传播的平面波的振幅可表示为：
A_x＝A₀e-^αx (6)其中A₀是在x=0处波的某一变量的振幅，如声压振幅、质点速度振幅或密度振幅。Ax为同一变量在x处的峰值。α为振幅衰减系数，其量纲为[L-1]。如果只讨论吸收作用的贡献，α为振幅吸收系数。Stoke-Kirchhoff经典吸收系数为：
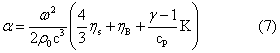　式中ω为角频率，η₃为切变粘度系数，ηB为体积粘度系数γ为比热的比，cp为恒压热容量，K为热导率。上述方程表示波通过具有一定粘度和热导率的媒质时波动过程传输的能量被转变为热。流体虽然不能支持静态切变，但能以粘度阻滞方式支持一种动态过程，从而由粘度引起损耗。介质中发生热传导过程是由于超声波通过时高声压强区的温度大于相邻的低压强区，对这一梯度发生响应，产生热量的流动。对于生物介质来说，热传导项远小于粘度项，故热传导项可忽略。式(7)表示吸收系数随频率的平方而变化，它与温度的关系遵循粘度的温度相关性。但是一般的液体尤其是生物材料并不总是有式(7)那样的简单关系，还必须考虑其中包括有丢失能量的其它弛豫过程。这类过程反映出存在着一些能量转移机理，这些转移机理是需要时间的。式(8)中A项代表经典吸收项，右边第二项描述一个弛豫过程，f，为弛豫频率

从第二项中可以看出，如果频率很低，波的周期远大于能量转移所需要的时间，则第二项便是常数，其值为B。如果频率很高，波的周期远短于能量转移所需要的时间，能量未从波动过程中被抽提出来，后一项消失，仅留下经典项。此外，只发生一个弛豫过程的情况是不多的，为了描述观察到的吸收谱，必须考虑几个弛豫过程，并将它们相加起来

图2表示由实验测量求得的生物材料的超声衰减系数与频率的关系。以每周的衰减相对于频率的对数作图。

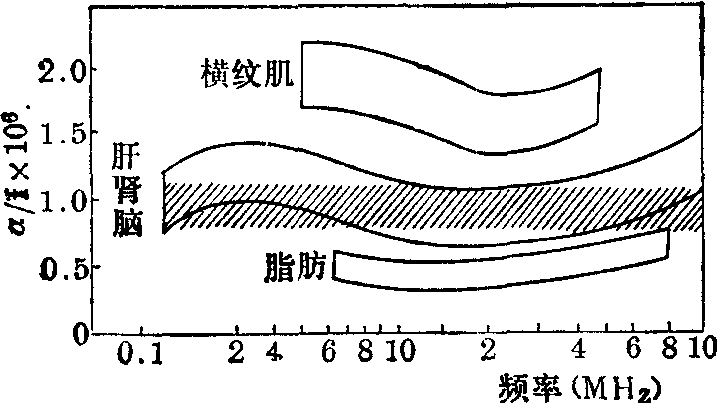
图2 哺乳动物组织每个波长的声振幅衰减(dB/cmMHz)系数与频率的关系

经典理论指出，如果衰减仅由吸收引起，则出现一线性关系（斜率为正）。由图可见在所考察的频率范围内每周的衰减一般是恒定的。哺乳动物肾组织的这种衰减与频率的依赖关系约持续到100MHz附近。此后以二次方关系占优势。脂肪的α/f值在1MHz～10MHz范围内略有随频率上升的趋势。横纹肌及肝组织的α/f值在2MHz附近有一最小值。
在介质对超声的衰减作用中有一部分是属于散射作出的贡献。如果靶体远小于超声波长，全部散射波向各方向均匀地散布(复杂结构的散射是它的组成单元散射的矢量和，这些组成单元必须足够地微小)，血细胞对超声的散射作用便属于这一类型。如果超声频率低于15MHz，血细胞的直径远小于波长。例如频率为5MHz时波长为0.3毫米，而红细胞的平均半径仅为2.75μm。这类散射是角相关的。考虑到血浆的粘滞性，血细胞的角散射用Ahuja公式描述：

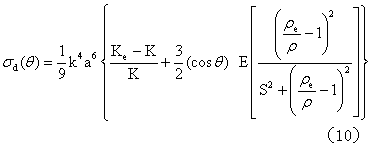
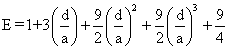
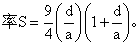式中σd(θ)为微分散射截面。单位立体角的散射功率是入射强度与σd的乘积，k=2π/λ,λ为波长，a为散射颗粒的半径(a<<λ), K为悬浮介质的绝热压缩系数，Ke为散射颗粒的绝热压缩系数，ρ为悬浮介质的密度，ρe为散射颗粒的密度，θ为散射角即平面波入射方向与散射方向间的夹角。vm为悬浮介质的粘度，ω为角频由式(10)可见血细胞的角散射依赖于压缩系数及悬浮介质与散射颗粒之间的密度差异。成年人正常血液中的红细胞个数远多于白细胞，红细胞的体积远大于血小板，所以对血液的超声散射作出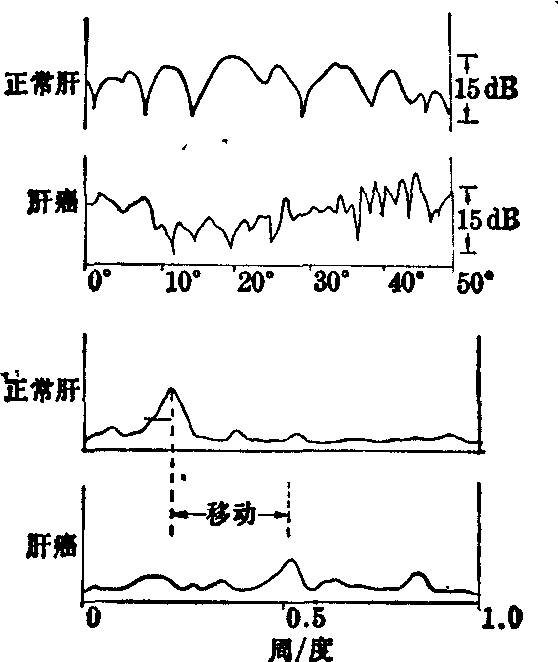

图3 组织的Bragg反向散射衍射图

主要贡献的是红细胞。另外这类散射也与频率相关的。在5MHz～15MHz范围内低血细胞比容全血的超声反向散射系数与超声频率的四次方成正比，符合瑞利散射理论。红细胞的15MHz超声散射截面约为它的几何投影面积平均值的10-4倍。血流中红细胞的超声散射是血流的超声多普勒信号源。通过测量软组织的超声散射频谱及超声反向Bragg衍射，可以研究散射能量与组织结构之间的关系(图3，下两图系对应于上两图的功率谱)。