素数

 凡数，他数度之不能尽，惟一可度尽者，谓之数根……
 屡乘求一考数根法：法以用数之诸方积，或大于本数，或大于半数之半者，与本数相减，馀为乘法，乘法自乘，或再乘，以本数度之，不尽，复以乘法乘之，以本数度之，如之递求。至不尽数为诸正数，或诸负数，而止。乃计共用乘法若干次，以次数乘用数之方数，为泛次。若不尽数为一，或一之负数，则泛次即定次，若为诸方积，或诸方之负数，则以其方数减泛次，为定次，以定次度本数。若所馀非一，则本数非数根。若馀一，则视定次为何二数相乘之积，其相乘数为偶者，即为递加数；为其者倍之为递加数，乃置一，加一递加数，再加一递加数，如此递加，以递除本数，恰尽即止。若至得数小于法，仍不恰尽，则本数是数根。如本数三百四十一，用数二之九方积五一二，大于本数，以本数减之，馀一七一，为乘法，自乘，得二九二四一，以本数度之，不尽二五六，为用数之八方积，计用乘法二次，以方数九乘之，得一八，以不尽之方数八减之，得一○,为定次，以度本数，馀一，定次一○,为二与五相乘积，倍五得一○,为递加数，以加一，得一一，以除本数，得三一，恰尽，则三百四十一非数根。
 

清·李善兰《考数根法》(《中西闻见录》第二号，1872年

 【评】《考数根法》是中国数学史上系统研究素数的第一篇论文。李善兰在此独立证明了著名的费尔玛素数定理(又称为费尔玛小定理)。

诉述；素数

◉ 诉述sùshù　动 诉说。〈例〉～经历/ 李奶奶向铁梅～了革命家史/ 祥林嫂反复向人～儿子阿毛遇难的经过。〈近〉讲述/ 诉说。
◉ 素数sùshù　名 也叫“质数”。在大于1的整数中，只能被1和这个数本身整除的数。〈例〉2、3、5、7、11这些数都是～。

素数sù shù

在大于1的整数中，只能被1和这个数本身整除的数。也叫质数。1930年《中华百科辞典》：“素数(Prime number): 凡数除一及本数之外不能以他任意数除尽之者，曰素数。”

素数sushu

即质数.

素数Sushu

又称质数。一个大于1的整数，如果除了1和它自身外，不能再被其他的正整数所整除，就称为素数。素数概念最初是由古希腊的毕达哥拉斯（参见该条）学派提出来的，它的产生不会晚于公元前400年。最初2并没有被看作一个素数，后来亚里士多德（参见该条）曾说2是 “唯一的素偶数”， 从此素数的概念就完备了。素数定义的最早明确记载见于欧几里得《几何原本》(约公元前300)第7卷定义11: “素数是只能为一个单位 (注： 即1) 所量尽者。”应该注意， “量尽”这个词，欧几里得的用法是仅在较小的数相对于较大的数时才使用的， 与今天的整除概念稍有区别。
有关素数的研究自从希腊数学以来一直是数论中最基本、最引人注目、最困难的课题之一。欧几里得已经认识到，素数是用乘法建立整个自然数系的基石，当然还应该考虑到1，对此他也是十分明确的。《几何原本》中给出了关于素数的一些最基本的定理，其中最精彩的是关于素数的个数（参见该条）的无限性的证明，书中还包括了关于自然数分解为素数的算术基本定理（参见该条）的实质性内容。公元前3世纪，埃拉托色尼(Eratosthenes)给出了逐个求出不大于正整数N的全部素数的筛法， 它实际上也是判定某一正整数是否为素数的方法。2000多年来，它一直是数学家们研究素数的最基本的工具， 并被从多方面作了推广。
数论中有许多极为重要和著名的问题与素数联系在一起， 许多至今仍未获得解决， 例如：
(1)是否存在无穷多个默森尼素数M_p＝2^p-1(其中p是素数。参见 “默森尼数”)?
(2)费尔马素数(参见 “费尔马数”)是只有有限个， 还是有无穷多个？
(3) 哥德巴赫猜想 （参见该条）。(4) 孪生素数猜想 （参见该条）。
(5) 相继素数差猜想： 两个相继的平方数n²及(n+1)2之间至少有两个素数。它是1855年由杰波夫(Desbores, A.) 提出的。
(6)是否存在无穷多个形如Rp (这里， R_p表示p个连写的1，其中p是素数7的素数？这类素数中，最小的一个是11。1904年， 在著名的 《坎特伯雷难题集》 中有 一个问题：1111111111111111111 (19个1连写)是不是素数？从此这类特殊的素数引起了人们的注意，后来证明，R₁₉确为素数，1929年，又有人证明R₂₃是素数。1977年，美国数学家威廉斯19个1连写是不是素数？从此这类特殊的素数引起了人们的注意，后来证明，R₁₉确为素数，1929年，又有人证明R₂₃是素数。1977年，美国数学家威廉斯(Williams,H. C.)证明了R₃₁₇是素数。1986年他又与人合作证明了R₁₀₃₁是素数。并且证明：下一个R_p形的素数如果存在，必定大于R_10000。关于形如R_n(n为大于1的整数)，一个明显的事实是：若R_n为素数，则n必为素数，反之却不然，例如R₃＝111=3×37。
此外如： 是否存在无穷多个形如n²+1或n²+k(k为正整数)的素数7?是否存在一个大于2的偶数，它不是两个素数之差？是否存在无穷多个形如n! +1或n! -1的素数？ 在斐波那契数列 (参见 “兔子问题”)中是否含有无穷多个素数？以及本世纪50年代以来提出的吉尔布瑞斯猜想（参见该条）和富顿猜想（参见该条）, 以及许许多多其他的未解决问题。
尽管素数的定义极为简单， 但是素数在自然数列中的分布却不服从任何简单的公式， 它们就像野草一样乱长，没有人能预报下一个素数会从哪里冒出来，在它们相互之间既可以具有任意大的间隔(参见“素数公式”)，但似乎又有无穷多对孪生素数。另一方面，又确实存在着关于素数的某种规律，任给正整数x，考虑不超过x的素数的个数，我们将其记为π(x)。1808年，勒让德在研究这个函数的性质时发现， 对于充分大的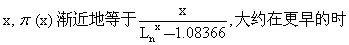
候高斯已经注意到在x充分大的时候， 素数的平均密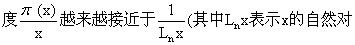
数)。这两个猜想都可归结为后人所说的“素数定理”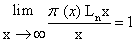：1896年， 法国数学家阿达玛 （参见该条）和比利时数学家瓦莱—普桑参见该条和比利时数学家瓦莱—普桑 (Vallee-Poussin,C. dela) 相互独立而又几乎同时证明了它。

素数

又称“质数”。在大于1的整数中，除1和自身外，没有其他正因数的数。其余整数称为合数。