等幂轴dengmi zhou

两个不同心的圆的幂相等的点的轨迹.等幂轴是垂直于连心线的一条直线.
设⊙O的半径为R,⊙O′半径为r,O与O′不重合，若P点关于⊙O,⊙O′的幂相等，则PO²-R²＝PO′²-r².可知P点的轨迹是垂直于连心线OO′的一条直线l.设OO′=d,O点到l的距离为d₁,O′，点到l的距离为d₂.则

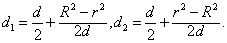
从以上原理可得以下三种情况：
❶相交两圆的等幂轴是通过两圆交点的一条直线（公共弦所在直线）.如图1,⊙O与⊙O′交于A,B两点，直线AB是它们的等幂轴；

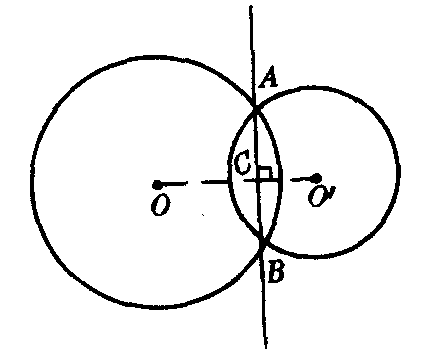
图1

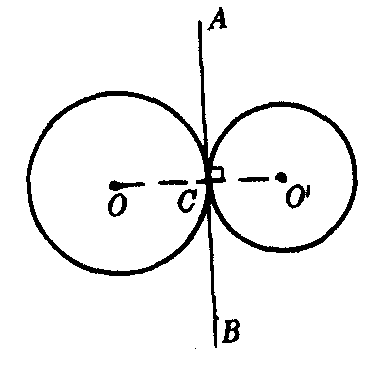
图2

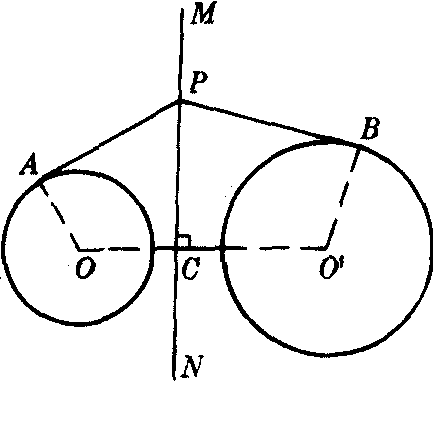
图3

❷相切两圆的等幂轴是过切点的公切线.如图2,⊙O,⊙O′切于C，过C点两圆的公切线AB(过切点垂直于连心线OO′)是它们的等幂轴；

❸没有公共点的两圆的等幂轴是过P点且垂直于连心线的一条直线，P点到⊙O,⊙O′的切线长相等.如图3.