空间坐标变换kongjian zuobiao bianhuan

指的是空间同一点关于新、旧坐标系的坐标间的变换公式。移动空间直角坐标系的原点而不改变坐标轴的方向和长度单位称为空间直角坐标系的平移。设空间任意一点P对于旧坐标系OXYZ的坐标为P (x,y,z)，对于新坐标系O′ X′ Y′ Z′ 的坐标为 (x′y′z′)，新原点O′ 对旧坐标系OXYZ的坐标为 (x₀,y₀,z₀)，则空间直角坐标系的移轴公式为： x=x′ +x₀,y= y′ + y₀,z=z′ +z₀。用P点的旧坐标表示它的新坐标的逆变换公式为： x ′=x-x₀ ,y ′=y-y₀,z′ =z-z₀。
不动空间直角坐标系的原点而转动坐标轴，称为空间直角坐标系的旋转。假定新坐标轴对于旧坐标轴的方向角，由下表确定，P为空间任意一点，它的旧坐

	OX′	OY′	OZ ′
OX	α1	α2	α3
OY	β1	β2	β3
OZ	γ1	γ2	γ3

标为 (x,y,z)，新坐标为 (x′y′z′)，则x= x′ cosα₁+y′ cosα₂+z′ cosα₃,y=x′cosβ₁+y′ cosβ₂+z′ cosβ₃,z=x′cosγ₁+y′cosγ₂+z′ cosγ₃。这称为空间直角坐标系的转轴公式。用P点的旧坐标表示它的新坐标的逆变换公式为：x′ =xcosα₁+ycosβ₁+zcosγ₁,y′ =x′cosα₂+ycosβ₂+zcosγ₂,z′ =zcosα₃ +ycosβ₃ + zcosγ₃。
将空间直角坐标系的平移和旋转变换结合起来，就得到一般的坐标变换公式

其逆变换公式

其中　x₀′ =- (x₀cosα₁ +y₀cosβ_l +z₀cosγ1 )
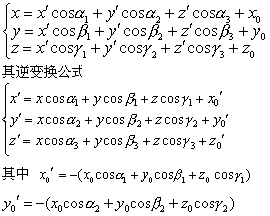
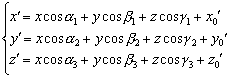
　y₀′ =- (z₀cosα₂+y₀cosβ₂+z₀cosγ₂ )
　z₀′ =-(x₀cosα₃ +y₀cospβ₃ + z₀cosγ₃)。