积分中值定理jifen zhongzhi dingli

若函数f(z)在闭区间上连续，则在[a,b]上至少存在一点c，使得

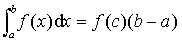
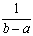
当函数f (x)在区间 [a,b]上连续时，常称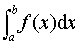为f (x)在 [a, b]上的积分平均值. 由积分中值定理可知，必存在c∈ [a,b]，使得f (c)等于f (x)在 [a,b]上的积分平均值.
积分中值定理的几何意义是，若f (x)≥0，则连续曲线y=f (x),x轴与直线x=a,x=b所围成的曲边梯形的面积等于以区间 [a,b]上某一点c的函数值f (c)为高，以区间 [a,b] 的长为宽的矩形面积，如图.

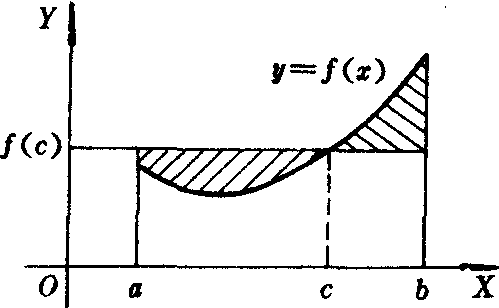
该定理的物理意义是，以连续变化的速度v(t)作直线运动的质点，自时刻t= a到时刻t=b所走过的路程，等于质点在同一段时间内以a与b之间的某时刻c的瞬时速度v(c)作匀速运动所走过的路程.

积分中值定理

函数f(x)在区间[a,b]上连续g(x)在区间[a,b]内可积且不变号，则在区间[a,b]内至少存在一个数ζ(a<ζ称为积分第一中值定理。若g(x)在区间[a,b]上可积，f(x)在[a,b]上是单调的，则在区间[a,b]内至少存在一个数ζ(a<ζ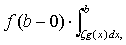称为积分第二中值定理。