种群增长模型population growth models

描述种群数量随时间变化的动态数学方程。自然界中昆虫种群的世代可以是不重叠或完全重叠的，数量的增长可能与种群密度无关或有关，因此描述种群增长的数学模型各异。
世代完全重叠模型 一年发生几十个世代的蚜虫类，种群世代完全重叠，种群数量即以连续的方式变化，其动态描述可用微分方程表达。
无限环境条件 若种群在无限环境条件下，种群增长与种群密度无关，且假设种群内的个体都具有同样的生态学特性，其数学模型为指数增长方程：

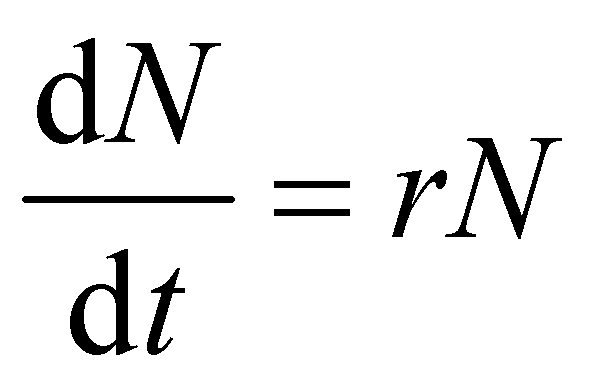
积分得： N_t＝N₀e^rt
式中 N表示种群数量；t表示时间；r=b-d表示种群的增长率，b、d分别表示种群的出生率和死亡率。当r>0时，种群呈无限指数增长，当r<0时，指数增长立即下降。此类种群增长呈J型生长型。
有限环境条件 若种群在有限环境条件下，则种群的增长与种群密度有关。其增长的基本特征可用逻辑斯蒂方程表示，其微分方程为：

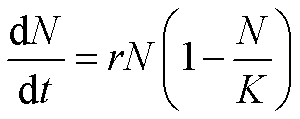
式中 K值为环境饱和量，如食物、空间、天敌等；r为与环境无关的种群增长率。rN(1-N/K) 项是种群有效增长率与种群密度关系的表示式。若NK时，dN/dt为负值，若N=K时，即出现一个完全稳定的种群平衡值。
逻辑斯蒂方程是包括3点假设： ❶在种群内所有个体都有同样的生态学特性，即所有个体的死亡、生殖、捕食或被捕食都是相同的，这样就不考虑年龄结构的影响；
❷在种群中所有个体都反映着它们在环境中瞬间的变化，即种群数量变化率是当时种群数量的函数，而与种群的过去无关，即：

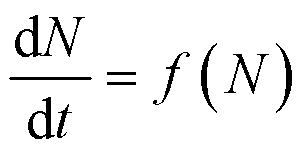
f(N)不是时间的函数；
❸在任何特定情况下，种群大小有其恒定的上限，并在任何特定时间内，种群增长率与该时种群大小和上限间之差成线性比例。
许多生活史复杂的物种，由于时滞的影响，在K值附近常出现颤动现象，逻辑斯蒂方程需作时滞修正。
世代不重叠模型 当种群世代不重叠时 （如每年发生一代的某些物种种群），则种群增长分步进行，对时间t不连续，数学模型应用差分方程。
与密度无关时 若种群增长与密度无关时，其数学方程为：
N_t+₁＝N_te^rt
或 N_t+₁＝λN_t
式中r=lnλ; 若λ>1时，上式表指数增长，若λ<1时，则表指数下降，以至消失。
与密度有关时 若种群增长与密度有关时，其数学方程为：
Nt₊₁＝F(Nt)=F(N)
式中 F(Nt) 是Nt的某种非线性函数，已有许多与逻辑斯蒂方程相似的不连续方程，结合生物学的特征，F(N)的形式见表：

F(N)的形式

代号	F(N)的形式	平衡点(N*)	TR(或1/r)
A	N[1+r(1-N/K)]	K	1/r
B	Nexp[r-(1-N/K)]	K	1/r
C	λN(1+αN)-β	(λ1/β-1)/2	[β(1-λ-1/β)]-1
D	λN1-b;(N>b) λN;(N	λ1/b	1/b

表中F(N)的4种形式有如下基本特征：在低密度时，种群有减少倾向，并有一个或几个参数衡量这个非线性反应的严峻性。
关于时滞问题，当TR>1(在A或B式中，1>r>0)时，有一个单调的阻尼稳定点； 当1>TR>0.5(在A或B式中2>r>1)时，有一个振荡阻尼稳定点，而当TR<0.5(在A式或B式中，r>2)时，有一持续而有界的振荡。TR=1/r为恢复时间或自然反应时间