位移有限单元法基本原理

---

线弹性结构小变形位移有限单元法的理论基础．是弹性理论和最小势能原理(或虚功原理)。

最小势能原理：在满足给定位移边界条件的所有位移中，只有满足平衡方程和面力边界条件的位移，可使弹性体的总势能π取极小值。

π=U－W (1．3－75)

式中 弹性体应变势能

❷ 在各个单元内，通过插值方法，将位移矢量｛u｝用1单元节点位移矢量｛q｝近似表示，即

｛u｝=〔H〕｛q｝ (1．3－77)

其中，〔H〕是插值函数矩阵。

再根据应变位移关系，得到应变矢量｛ε｝与单元节点位移矢量｛q｝的关系

｛ε｝=〔L〕｛u｝=〔L〕〔H〕｛q｝=〔B〕｛q｝

(1．3－78)

其中，〔L〕为弹性理论的应变位移关系式中微分算符矩阵，〔B〕=〔L〕〔H〕为应变矩阵。

❸ 计算单元势能п_e，求单刚矩阵〔k〕和单载矢量｛Q｝：

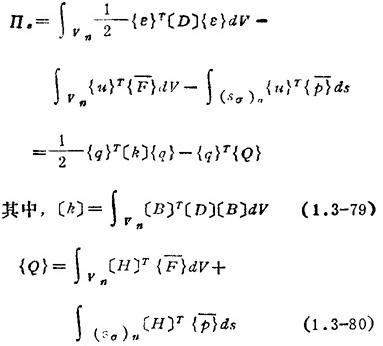
❹ 计算弹性体总势能Π：

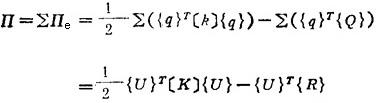
组集单刚矩阵和单载矢量成总刚矩阵〔K〕和总载矢量｛R｝，其中｛U｝是总体节点位移矢量。

❺ 根据弹性体总势能Π的极值条件，得到总体刚度方程组。

弹性体总势能Π是各个节点位移分量u₁、v₁、ω₁、u₂、v₂、ω₂、……的多元函数，其极值条件是：

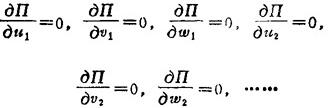
用矩阵形式表示为：

〔K〕｛U｝－｛R｝=0或〔K〕｛U｝=｛R｝

(1．3－81)

❻ 根据给定位移边界条件修正总体刚度方程〔K〕｛U｝=｛R｝，求解得到总体节点位移矢量｛U｝。

❼ 由已知单元节点位移矢量｛q｝，求单元应力：

｛σ｝=〔D〕｛ε｝=〔D〕〔B〕｛q｝=〔S〕｛q｝

(1．3－82)

其中 〔S〕=〔D〕〔B〕是应力矩阵。

如果用虚功原理来推导有限元方程，结果相同，仅上述第❸ 、❹ 、❺ 步略有不同，即

第❸ 步计算单元虚应变能dU_e和虚功δV_e。得到单刚矩阵〔k〕和单载矢量｛Q｝

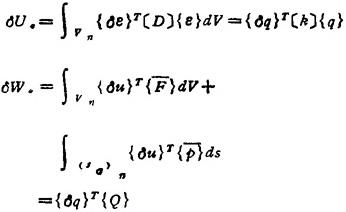
第❹ 步计算弹性体总虚应变能dU和总虚功δW，组集成总刚矩阵〔K〕和总载矢量｛R｝

δU=∑(δU_．)=∑(｛δq｝^T〔k〕｛δq｝)=｛δU｝^T〔K〕｛U｝

dW=∑(δW_e)=∑(｛δq｝^T｛Q｝)=｛δU｝^T｛R｝

第❺ 步由虚功方程δU=dW，得总体刚度方程组

｛dU｝^T〔K〕｛U｝=｛δU｝^T｛R｝

由于总体虚位移矢量｛δU｝是任意的非零矢量，上式可写成：

〔K〕｛U｝=｛R｝