相关分析analysis of correlation

度量各因素间互相影响的密切程度的统计方法。相关分析不将因素区分为自变量与依变量，只用特定的统计数表示因素的相关程度。相关分析在农业化学研究中应用十分广泛。
相关系数 又称简单相关系数，是度量两个因素密切程度的统计数，符号为r。

式(1) 分子部分称为协方差，分母根号内分别为因素x、y的平方和，相应的协方差与平方和简作l_xy、l_x、l_yy。相关系数是无单位的纯数。取值范围自-1至1。当相关系数为正值、负值及零时分别称为正相关、负相关及无相关。
相关系数的显著性检验 样本相关系数r为从总体相关系数为ρ的总体中抽取的随机样本。若ρ=0,r将出现在0周围呈对称分布。显著性检验可取无效假设H₀:ρ=0，相应的备择假设为H_A:ρ≠0，作自由度为N-2的检验。已将信度α=0.05及α=0.01的显著水平下的临界ra值列成表格备查。如r≥ra，则在α显著水平下接受H_A:ρ≠0，否则接受H₀:ρ=0。
当ρ≠0且样本容量N较小时，r的分布不对称。为了使r分布接近于正态分布，取反正切双曲函数变换，并称之为Z。

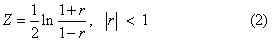
不论总体相关系数ρ为何值，Z的分布都近似于正态分布。将r转换为Z用于检验r与ρ差异的显著性；检验两个相关系数的显著性，求几个相关系数的平均值。
决定系数 相关系数r的平方值r²。可表示为：

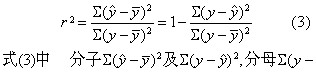
ȳ)²分别为线性回归中的回归平方和、剩余平方和与总平方和。决定系数就是回归平方和占总平方和的比例。当相关系数r=0.6时，因素x对因素y的影响不是60%，而是其平方值36%。用决定系数r²来解释两因素的相关程度意义清楚、不致发生夸张结论，而且r2的计算比r简单。但r²的取值区间为[0,1]，无正负号区别，不能表达出相关的性质，故r与r2常结合应用。
复相关与偏相关 在多元回归分析中因素x的数目为i、j=1,2,3，…，p;(iy·12…p表示，由式(3)拓广得：

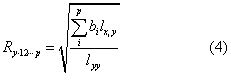
式(4)表明复相关系数的取值区间为(0、1)。
对复相关系数的统计假设测验为H₀:ρ_y·12…p＝0，相应的备择假设为H_A:ρ_y·12…p≠0，可用F测验其显著性，已将相应自由度f₁、f₂的信度为α=0.05及α=0.01，临界R_a值列成表备查。若R≥Ra则在显著水平为α下接受H_A，否则接受H₀。
当p-1个因素取固定不变状态时，剩余的一个x因素与y因素的相关系数称为偏相关系数或净相关系数。偏相关系数通常以r_{12·34…p、p+1}表示，下标黑点后的数字代表固定不变的因素，黑点前的数字代表相关的因素。当因素数较多时常简记作r_ij,(i,j=1,2，…，p,p+1j

式(5)中 C为p+1阶相关系数矩阵的逆矩阵R^-1＝C的元素。偏相关系数的显著性检验用t测验，假设总体偏相关系数p_ij为零，即H₀:ρ_ij＝0，其备择假设为H_A:ρ_ij≠0，并计算出显著水平为a的临界r_a值作比较，r_ij≥r_a接受H_A，否则接受H₀。
相关系数r与偏相关系数rij不仅取值不等，有时正负号也可能不一样。相关系数r未排除其他因素的干扰，例如土壤中养分转化量在适当范围内受温度、水分条件增加而加速，但降雨或灌溉常伴随着温度下降。由于温度与水分间存在相关性，因而温度对转化量及水分对转化量的相关产生干扰。偏相关系数则是固定温度不变的条件下研究水分对转化量的相关系数，或固定水分不变的条件下研究温度对转化量的相关关系。偏相关系数能更客观地评价因素间的相关关系。

---

相关分析xiangguan fenxi

见统计分析。

相关分析

用一些合理的指标对相关变量的观察值进行统计分析。常被应用于测验分析统计中。

相关分析xiang guan fenxi

考察两列变量之间关系的统计方法，反映不同现象之间是否有关系，关系程度如何。相关的情况有三种，即正相关、负相关和零相关。在研究中用相关系数(r)表示两列变量之间的相关程度。它只是一个比率，不代表相关的百分数，更不是相关量的等单位度量。相关系数的数值介于-1.00—+1.00之间，数值前的正负号表示相关方向。相关系数的绝对值越大，相关程度越高。最常用的相关为积差相关和等级相关。

相关分析

数理统计的一个内容。分析两个（或多个）变量之间相互关系的密切程度。把这种相关性用数值表示，称此数值为相关系数。把变量之间的关系用函数表示，称为回归分析。所得函数表达式称为经验公式。经验公式中使用直线方程时称为线性回归。在工农业生产管理和科学实验中数据处理通常结合使用相关分析和回归分析。

相关分析

利用概率方法对密码变换过程中各种因素相关特性的分析。

相关分析correlation analysis

即对相关关系的分析，包括计算相关系数、进行相关系数的假设检验等，借以了解两种事物或现象数量变化的相互关系，包括相关性质、相关程度及相互关系的存在与否。

相关分析Correlation Analysis

研究两个或两个以上处于同等地位的随机变量间相关关系的一种统计分析方法。如人的身高和体重之间、空气中的相对湿度与降雨量之间的相关关系都是相关分析研究的问题。相关分析与回归分析之间有联系，但各自侧重点不同，回归分析侧重于研究随机变量间的依赖关系，以便用一个变量去预测另一个变量。相关分析侧重于发现随机变量间的种种相关特性。相关分析在工业、农业、生物学、水文、气象、社会经济等方面都有应用。

相关分析

研究变量之间关系紧密程度的统计分析方法。直线相关用相关系数表示，曲线相关用相关指数表示。相关分析的任务，是要透过大量的偶然现象去发现事物的必然规律，使人们对现象之间相互依存关系的认识由定性进入定量，因而使这种认识进一步具体和深入。这种定量的规律性的认识，是进行估算和预测的科学依据。进行相关分析首先要对现象间是否存在相关关系，存在何种具体形式的相关关系作出初步的定性判断和认识。即根据自己的专业知识、理论知识、实践经验和逻辑推断，来分析和判断事物之间是否相关，如何相关，这是相关分析的起点。紧紧抓住事物间的本质联系，才能使相关分析沿着正确的方向进行下去。其次是确定相关关系的密切程度，主要方法是绘制相关图、计算相关系数或相关指数等。相关分析与回归分析结合，是对现象之间变量关系统计研究的主要内容

相关分析

研究变量间关联程度的一种统计方法。它与回归分析是密切相联的概念。回归分析给出估计的回归方程及其因果关系，而相关分析则给出一系列的指数，如相关系数，复相关系数。它并不关心其间的因果关系。尽管相关分析作用不如回归分析，然而，它是回归分析的辅助工具。有些著作把两者统称作回归分析或相关分析。相关可分作： 简单相关与多重相关，线性相关与非线性相关，或是正相关、负相关与无 （零） 相关等。在人寿保险中，相关分析可用于研究收入水平与寿命、收入水平与投保业务发展等关系问题，也可以用于回归模型的有效性检验。

相关分析correlation analysis

一种确定变量间相关关系密切程度的统计方法。研究变量之间相关关系的关联程度。

相关分析

根据实际观察和社会调查所获的数据资料分析现象之间相关关系的程度和形式的一种统计分析方法。相关分析的主要任务是用数学公式来表达某一种标志值发生变动时，另一种有联系的标志值会如何发生相应的变动这一相关关系。一般采用分析分组法。应用分析分组法时，首先要对被研究总体的各单位标志值进行分组，其次要构成能体现各有关标志值相互依存关系的数列。计算各单位标志值相互依存关系时，可以利用有关的数学公式对现象标志间关系的紧密程度及其形式进行测定。相关分析的主要内容有：（一）确定现象之间有无关系，确定相关关系的表现形式（直线相关还是曲线相关）;（二）确定相关关系的密切程度，即计算相关系数来说明相关关系的密切程度；（三）测定两个变量之间的一般关系值，即建立函数关系的近似表达式，并作为判断、推算和预测的依据；（四）测定因变量的估计值（理论值）和实际值之间的差异，并计算估计标准误，用来反映因变量估计值的可靠性。

---

相关分析

根据系统的大量资料，确定系统某些量之间的相互关系，即相关程度大小以及函数关系的理论和方法。“相关”一词源出统计学，由英国的弗朗西斯·哥尔登爵士首先提出，哥尔登族人由“相关”概念创立了相关分析法。现象之间的相互关系按相关程度有不相关、不完全相关、完全相关。相关分析的主要对象是不完全相关。按相关的性质有正相关与负相关：一个变量随另一个变量的增加而增加为正相关；一个变量随另一个变量的增加而减少为负相关。按相关的形态有直线相关和曲线相关：在相关图上，相关点散布在一直线附近两旁为直线相关；如果散布成曲线流动为曲线相关。从相互影响的因素多少有单相关与复相关；一个因变量对一个自变量的相关关系为单相关；一个因变量对两个或两个以上的自变量的相关关系为复相关。相关分析简单的方法是相关图法。将相关因素分成几对，把每对数值用点子填列在直角坐标图上，根据点子出现的规律，判断现象之间的相关关系。复杂的方法是相关方程和相关系数的计算。相关分析在工业、农业、水文、气象等方面均有应用。新闻传播系统的诸因素既有正相关，也有负相关，有单相关，也有复相关。如事实材料的数量多与新闻信息量可能是正相关，也可能是负相关。新闻事实多就成正相关，新鲜事实少，旧的事实多，就成负相关。整个新闻系统的传播效率由主导因素的相关作用决定，对主导因素进行相关分析是认识新闻系统结构与功能的方法。对于难以定量的新闻现象之间的相关分析可用逻辑关系进行定性分析。

相关分析

研究事物随机变化的两种现象或多种现象间相互依存关系的一种数学分析方法。其主要任务是确定变量之间是否存在相关关系以及这种关系的密切程度。它是根据关系的形式建立关系方程式，用以反映变量之间的依存关系，定性地分析相关关系。为了定量地分析两个随机变量相关程度，要计算它们的相关系数，并按其数值大小确定相关关系的密切程度。相关关系有多种类型。按其所涉及标志的数量，可分为单相关和复相关。单相关研究两个标志之间的关系，复相关研究两个标志以上的关系。按其变化的方向，可分为正相关和负相关。前者是两标志间数量变化方向相同，后者是两标志间数量变化方向相反。另外，按其相关关系的形式，可分为线性相关和非线性相关。前者能用线性函数作近似表示，后者则不能用线性函数表示。进行相关分析的方法较多，通常有散列表、散列图、分析分组、回归等。相关分析广泛地应用于经济数量分析。

相关分析correlation analysis

两个或两个以上随机变量之间相互关系密切程度的分析。两个变量之间的相关关系称简单相关关系。以直线为准的相关分析为线性相关分析。例如，分析变量x、y之间线性相关关系，从样本的n次观测值(x_i,y_i;i=1,2，…，n)，可以计算x和y之间的关系程度的度量，称为相关系数，用r表示：

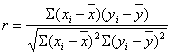
式中和y分别是x、y观测值的平均数。r满足-1≤r≤+1,|r|的大小表明x、y线性关系密切的程度，r取正值为正相关，r取负值为负相关。由r对总体相关系数ρ作检验，即检验H₀:ρ=0,H₁:ρ≠0时，可用t统计量，t=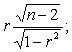检验H₀:ρ=ρ₀≠0,H₁:ρ≠ρ₀时，检验量可用近似正态分布的Z量，Z=(1/2)1n((1+r)/(1-r))。在曲线为准的相关分析中，计算x和y之间的关系程度的度量，称为相关指数。
两个以上变量间相互关系密切程度的分析为复相关(multiple correlation)分析。类似地可计算复相关系数R,y对x₁,x₂，…，x_m的复相关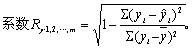常用F检验量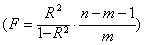作H₀:ρ=0的检验。在多变量情况下，变量间的相关关系错综复杂，为了确切表示两个变量间的相关关系，需要在消除其他变量影响的情况下，来计算其相关系数，即偏相关(或净相关，partial correlation)系数。偏相关系数的一般计算式是：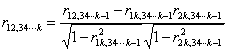

对以上任何一个偏相关系数，都可以用相应的t统计量作相应总体偏相关系数为零的假设检验。通过偏相关分析，可选择对因变量影响大的自变量，舍弃影响小的自变量，以便反映现象间的主要联系。

相关分析

分析变量之间数量关系的统计方法。根据观察资料，在定性分析基础上，运用数学方法，对变量之间相关关系的密切程度作定量描述。相关关系是变量之间存在的非严格的、不确定的数量关系，如身高与体重的关系，农作物收获率与施肥量、降雨量的关系。在有相关关系的变量中，作为根据（或原因） 的变量称为自变量，作为发生对应变化（或结果） 的变量称为因变量。例如，施肥量、降雨量为自变量，收获率为因变量。两个变量之间的相关，称为单相关或一元相关，多个变量之间的相关称为复相关或多元相关。在多变量情况下，保持其他变量不变仅分析其中两个变量之间的相关称为偏相关。变量之间的关系表现为直线的称线性相关； 否则，称为非线性相关。相关分析中最常用，最基本的是线性相关。相关分析最简单的方法是散点图。把变量值用小圆点表示在方格纸上，根据圆点分布的集散及形状，来分析变量之间有没有相关关系及相关的密切程度。为了从数量上更确切表明变量之间的相关形式、程度，必须计算相关系数。

相关分析correlation analysis

研究现象或变量之间是否存在某种依存关系，并探索存在依存关系现象的相关方向以及相关程度的统计分析方法。一般通过相关系数的计算来反映不同现象或变量之间相关关系。主要形式有： (1) 线性相关分析，研究变量间线性关系，一般用相关系数r来描述；(2) 偏相关分析，研究变量间线性相关关系时，控制其他可能对此关系产生影响的变量；(3) 距离分析，测度观测量之间或变量之间相似或不相似程度。

相关分析

根据样本数据分析变量之间相关情况的统计分析方法。包括绘制散点图、计算相关系数、作相关显著性检验。