直圆锥面
直圆锥面zhiyuanzhuimian
已知一定直线上的一定点，过空间任意一点与定点作直线，使与定直线所成的锐角永远相等的动点的轨迹. 此定直线叫做直圆锥面的轴，定点叫做直圆锥面的顶点，定锐角叫做直圆锥面的半顶角. 直圆锥面也可看成是由曲线所产生的，已给平面π上一个圆C及垂直于平面π且过圆心的直线a上一点A (不在π上). 若直线l运动时，总经过A点且和圆C相交，则直线l所产生的曲面叫做直圆锥面，A点叫做顶点，圆C叫做准线，直线l所在的每一个位置叫做母线. 以P=P0+tS0为轴，P0为顶点；θ为半顶角的直圆锥面方程的向量形式是| (P—P0) × S0|=sinθ | P—P0 |. 坐标形式是
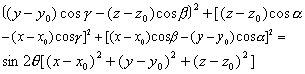
☚ 柱坐标系 直纹曲面 ☛
- 陆子寿是什么意思
- 陆子才是什么意思
- 陆子方是什么意思
- 陆子明是什么意思
- 陆子欣是什么意思
- 陆子正是什么意思
- 陆子渊是什么意思
- 陆子玄是什么意思
- 陆子真是什么意思
- 陆子美是什么意思
- 陆子芬是什么意思
- 陆子隆是什么意思
- 陆子青是什么意思
- 陆子静是什么意思
- 陆子馀集是什么意思
- 陆孝佩是什么意思
- 陆孝夫是什么意思
- 陆孝廉是什么意思
- 陆孝彭是什么意思
- 陆孝栋是什么意思
- 陆孟庄是什么意思
- 陆孟略是什么意思
- 陆季弘是什么意思
- 陆季疵是什么意思
- 陆季皋是什么意思
- 陆季衡是什么意思
- 陆学
是什么意思 - 陆学与道学是什么意思
- 陆学善是什么意思
- 陆学士杂著是什么意思
- 陆学艺是什么意思
- 陆学藩是什么意思
- 陆学钦是什么意思
- 陆学锦是什么意思
- 陆宅之是什么意思
- 陆守伦是什么意思
- 陆守经是什么意思
- 陆安是什么意思
- 陆安道是什么意思
- 陆完是什么意思
- 陆宏是什么意思
- 陆宏定是什么意思
- 陆宏绪是什么意思
- 陆宗九是什么意思
- 陆宗文是什么意思
- 陆宗林是什么意思
- 陆宗泰是什么意思
- 陆宗舆是什么意思
- 陆宗达是什么意思
- 陆定是什么意思
- 陆定一是什么意思
- 陆定圃是什么意思
- 陆宝是什么意思
- 陆宝忠是什么意思
- 陆宝树是什么意思
- 陆宝淦是什么意思
- 陆宝铎是什么意思
- 陆宝麟是什么意思
- 陆宠廷是什么意思
- 陆宣公奏议全集是什么意思