生统遗传学
生物统计遗传学的简称。用生物统计方法研究遗传的遗传学分支学科。
生统遗传学
生统遗传学
生物统计遗传学简称生统遗传学。是用生物统计方法研究遗传学问题的一门学科。这学科包括的内容很多,如数量性状遗传的研究,基因在群体中的行为的研究等。现仅就医学遗传学中比较容易碰到的几个问题加以讨论。
基因频率的估计 群体中某一特定位点上的基因频率可以从调查得的基因型频率算出来。设有等位基因A1和A2,由它们所组成的基因型A1A1、A1A2和A2A2。假设这三种基因型都能在表型上予以辨别,例如对100个个体进行调查后得出表1的数字:
表1 一对等位基因时基因型频率和基因频率的计算

由于每个个体含两个等位基因,在100个个体的200个基因中,110个是A1,90个是A2,所以A1的基因频率p=110/200=0.55,A2的基因频率q=90/200=0.45。不难看出,在基因频率p、q和基因型频率P、H、Q之间的关系公式为:
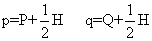
例如在M-N血型系统中,M血型和N血型分别代表两个纯合的基因型,MN型则代表杂合的基因型。现如在某地区调查了747人,从结果算出M血型占31.2%,N血型占17.3%,MN血型占51.5%,据此则P=0.312,H=0.515,Q=0.173,于是:
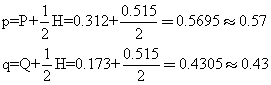
使用上法估计基因频率,必须调查出三种基因型的全部频率。因此,此法不适用于有隐性等位基因的情况,因其杂合体与显性的纯合体无法区别。在此情况下,假如群体就这对等位基因而论,已经达到Hardy-Weinberg平衡(见“群体遗传学”),那么仍然有办法从调查结果推算出p和q的估计值。所谓Hardy-Weinberg定律有以下几个要点:
❶在没有迁移、突变和选择的情况下,一个大的随机婚配群体,不论是基因频率或是基因型频率,都是稳定的,可以一代代保持下去。
❷一个处于Hardy-Weinberg平衡状态下的群体,在任何一代中的基因频率与基因型频率之间,都具有以下的关系:
P=p2,H=2pq,Q=q2
如果由于A1对A2为显性而使A1A1和A1A2在表型上无从区别的话,则:
P+H=p2+2pq,Q=q2
这样我们就可以从调查得到的A2A2的基因型频率Q来估计q了。即: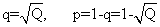
例如人类的白化症可能是由一对常染色体隐性基因纯合而产生的,在人类群体里,白化症的发生频率约为1/20,000=q2,故可算出:
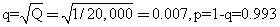
对于复等位基因,只要群体已达到Hardy-Weinberg平衡,对各个基因频率也可以从调查结果予以估计,例如人类的ABO血型系统是由三个等位基因IA、IB、i组成的。现举例介绍其基因频率的估计法如下: 有人调查了190,177人的血型,其结果如表2。表中设基因IA的频率为p,基因IB的频率为q,基因i的频率为r。
表2 ABO血型系统的理论频率和实得频率
| 基因型 | IAIA IAi | IBIB IBi | ii | IAIB |
| 血 型 | A | B | O | AB |
| 理论频率 实得频率 | p2+2pr 0.41716 | q2+2qr 0.08560 | r2 0.46684 | 2pq 0.03040 |
r2=0.46684,∴r=0.683
其次,可以看到B型和O型频率相加乃是:q2+2qr+r2=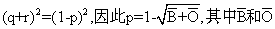 分别代表B型和O型的表型频率,即得:
分别代表B型和O型的表型频率,即得: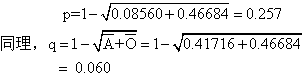
基因IA: p=0.257或25.7%
基因IB: q=0.060或6.0%
基因i: r=0.683或68.3%
总计:p+q+r=1或100%
系谱概率 概率是可能性或机遇的定量度量,譬如说有人怀了孕,生下来是男是女尚未可知,但是凭理论和经验,是男是女的可能性或机遇大约各有一半,也就是说生男的概率P(生男)=0.5,生女的概率P(生女)=0.5。类此生男、生女称为互不相容的事件,互不相容的可能事件有时不止两种,例如上节中的A、B、O、AB四种血型就都是互不相容的。概率还可从群体通过随机抽样所得的调查结果频率估计之。在上述ABO血型调查中,如在同一群体随机找一个尚未验过血型的人出来,那么,在未验之前就可以说他的血型为A的可能性为0.417,写成:P(A)=0.417,同样可以写出他的P(B)=0.086,P(O)=0.467,P(AB)=0.030(都只取3位有效数字)。如果事件C与早先出现过的事件D有关联的关系,则在发生了事件D的条件下发生事件C的概率称为条件概率,记为P(C/D)。反之,如C在D先,则在发生了事件C的条件下发生事件D的条件概率记为P(D/C)。条件概率的定律为:
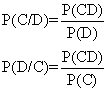
从条件概率的定律可以延伸出一个Bayes逆概率定理: 设事件D1,D2,D3,… Dn是互不相容的事件,设事件C跟这K个D事件中的第一个Di事件有关联,则各Di(i=1,2,……k)的条件概率为:
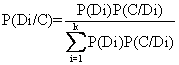
举计算系谱概率的例子:自毁容貌综合征是X连锁遗传的,患者有严重的精神障碍和运动紊乱,往往在幼儿期死亡。有一妇女(T)的两个舅舅有这种病(图1),如果她生一儿子,则儿子是否有病?从图1可以看到,R生了两个有病的儿子,所以R是杂合体,带有一个致病基因。同时又知道,R的女儿(S)有1/2的机会由遗传得到这个基因; 而R的外孙女(T)有1/4的机会由遗传得到这个基因。但T有4个正常的弟弟,能够对T的基因型提供另外的信息吗?因为S有4个正常儿子,所以她更可能是纯合体,而不是杂合体。我们用N代表正常基因,n代表致病基因,现在可以用Bayes公式来进行计算。
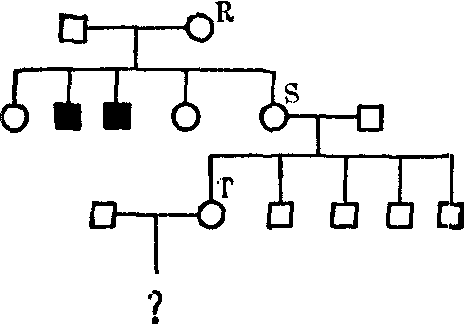
图1 自毁容貌综合征系谱(X连锁遗传)
表3 根据不同假设,计算条件概率
| 可能的假说 | C(4个男孩都正常) | P(C/Di) |
| D1:S是杂合体(Nn) | 1/2×1/2×1/2×1/2 | 1/16 |
| D2:S是纯合体(NN) | 1×1×1×1 | 1 |
表3中C代表4个男孩都正常的事件。如果S的基因型是Nn,那么S有4个正常儿子的概率是(1/2)4,所以P(C/Di)=1/16;如果S的基因型是NN,那么4个儿子当然都是正常的,所以P(C/Di)=1。
其次,我们知道R是杂合体,所以S是杂合体Nn和纯合体NN的机会各为1/2。从而
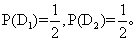 根据这些,可以算出Bayes 公式的分子为:
根据这些,可以算出Bayes 公式的分子为:
最后把这些数字代入Bayes公式,算出这系谱的概率如下:
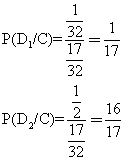
因为S生了4个正常儿子,所以可能性是16:1,那就是说,S很可能是NN而不是Nn。她是携带者的机会已由1/2降到1/17,因为她的4个正常儿子提供了另外的信息。从而T是携带者的概率是1/34。如果T有一个儿子,他是自毁容貌综合征的机会是1/68,或者说低于1.5%。
近婚系数 是表达近婚程度的度量。在近亲婚配中,原来因杂合而没有表现的隐性病基因从共祖先通过父母的渠道而在子代中纯合的可能性比一般婚姻的为大,使得病基因纯合体的表现概率在近亲婚配所产的子代中也大为增大。因此,对于近亲婚配近到什么程度的度量引起了婚姻咨询工作的重视,其度量值以近婚系数(F)表达之。F值可以从个体的系谱调查结果推算之,只需循谱追踪到他父母的共祖先,然后估计在每个分离上的概率,通过概率相乘和概率相加的定理,就可以计算出该个体的近婚系数F的值。如:一个个体的双亲P1和P2是嫡表兄妹,而下面系谱所示者,P1的母D和P2的父F是同胞兄妹(图2)。
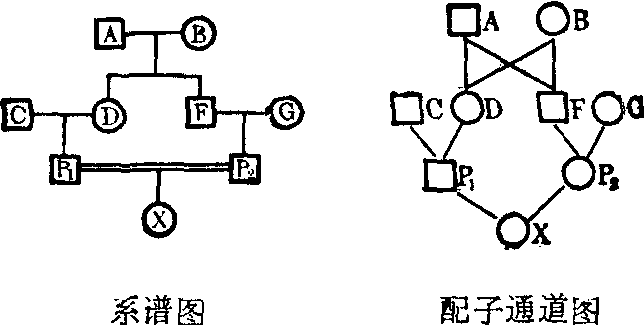
图2 一个近亲结婚的家系及其配子的通道图中□=○表示近亲结婚
先作系谱图,然后绘制共祖先的配子通道图。图中每一个体用字母标明,配子通道图中每根直线代表配子的通道。追踪双亲P1和P2联到共同祖先A和B的通道。共有两条通道把P1和P2联起来,一条是P1DAFP2,另一条是P1DBFP2。当A的某对等位基因a1和a2分配在他的配子中时,在一配子得到a1的概率也是1/2,因此D和F从A获得同样基因的复制品的概率是1/2,这是因为D得a1,同时F也得a1的概率是1/2×1/2=1/4,D得a同时F也得a
 的概率也是1/4,两者相加得D和F从A获得同样的a1或者同样的a2的概率为1/4+1/4=1/2,这个同样的基因a1或a2从D分离一次传给P1,概率小了一半,再分离一次传给X,概率又小了一半。所以传到X时,他从A得到两个同样的a1或两个同样的
的概率也是1/4,两者相加得D和F从A获得同样的a1或者同样的a2的概率为1/4+1/4=1/2,这个同样的基因a1或a2从D分离一次传给P1,概率小了一半,再分离一次传给X,概率又小了一半。所以传到X时,他从A得到两个同样的a1或两个同样的a2的复制品的概率为
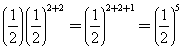
 其中n1是从一个亲体追踪到共祖先的世代数,n2是从另一亲体追踪到同一共祖先的世代数。在本例中n1+n2就是通道P1DAFP2中联系的数目n=n1+n2=2+2=4。上式于是可简写为
其中n1是从一个亲体追踪到共祖先的世代数,n2是从另一亲体追踪到同一共祖先的世代数。在本例中n1+n2就是通道P1DAFP2中联系的数目n=n1+n2=2+2=4。上式于是可简写为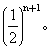
同理,X从另一共祖先B得到两个同样等位
基因的概率在本例中也是1/32。因此,X不论从A或从B得同样等位基因的概率是两个1/32之和,即
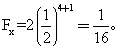 推而论之,一个个体的父母近婚系数的通用公式可以写为:
推而论之,一个个体的父母近婚系数的通用公式可以写为: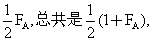 因此在共祖先A的通道P1DAFP2中的概率分量须改写成(1+FA)
因此在共祖先A的通道P1DAFP2中的概率分量须改写成(1+FA)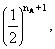 通用的计算近婚系数Fπ的公式因此是: Fx=
通用的计算近婚系数Fπ的公式因此是: Fx=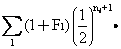
假定在以上所举的例子中,两个共祖先A和B都是亲表兄妹所生,他们分别有FA=FB=1/16,那么,用上式就可以计算出:

这比原先当FA=FB=0时,Fx=0.0625略大些。这个概率值说明个体X的任一位点上的基因对“后裔同样”的可能性,它可以用来估计他所拥有的全部基因中属“后裔同样”的基因对所占的百分率。因此,共祖先A和B所携带的隐性病基因愈多,在X身上表现出某种遗传病的可能性愈大,例如A和B不带任何病基因,那么X即使有6.64%的“后裔同样”的纯合体基因对,他也不会患任何遗传疾病。但据一般估计,我们每个人都或多或少地携带2~3个乃至7~8个处于杂合状态中的隐性病基因,所以要是A和B总共有10个致病基因与正常基因以杂合状态散布在10个不同位点上,那么X表现一种以上的遗传病的可能性为:

χ2检验法 为了描述在遗传理论预期数与调查或实验计数之间的吻合程度,需采用一种数理统计方法。这种方法称为χ2检验法。χ2是统计量,它的定义公式是:

表4 χ 2 简 表
| P v | 0.95 | 0.80 | 0.60 | 0.40 | 0.20 | 0.05 |
| 1 2 3 4 6 8 10 | 0.004 0.1 0.4 0.7 1.6 2.7 4.9 | 0.06 0.5 1.0 1.7 3.1 4.6 6.2 | 0.3 1.1 1.9 2.8 4.7 6.5 8.3 | 0.7 1.8 2.9 4.0 6.3 8.5 10.6 | 1.6 3.2 4.6 6.0 8.6 11.0 13.4 | 3.8 6.0 7.8 9.5 12.6 15.5 18.3 |
因此通过对χ2值的计算,就能以一定的概率推断在理论数与实计数之间的吻合度。表4中ρ为概率,v为自由度。在遗传学的实用例中,自由度一般等于类别数减去一。例如有人调查了1279人的三种类型MN抗原的人数分布如下:
nMM 363人——(实计数)1
nMN 634人——(实计数)2
nNN 282人——(实计数)3
n总 1279人
在共显性遗传,并且遗传受一对基因控制的理论假设下,M和N基因频率的估计量p和q分别为:
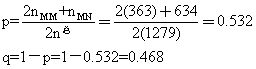
在群体已达Hardy-Weinberg平衡的理想假设下,以上三数类型的预计人数应为n(p+q)2的展开项,他们依次为:
np2=1279 (0.532) 2=361人——(预期数)1
2npq=2 (1279)(0.532)(0.468)=637人——(预期数)2
nq2=1279 (0.468)2=280人——(预期数)3于是用计算x2的公式算出:
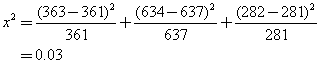
☚ 发生遗传学 群体遗传学 ☛
- 月下老儿是什么意思
- 月下老兒是什么意思
- 月下老定世间配偶是什么意思
- 月下老(月下书)是什么意思
- 月下老翁是什么意思
- 月下花前是什么意思
- 月下谁家笛,城头几片云。是什么意思
- 月下谈禅是什么意思
- 月下赛跑是什么意思
- 月下过秦岭,云中望剑阁。是什么意思
- 月下部是什么意思
- 月下钓鱼是什么意思
- 月下风前是什么意思
- 月下风前,应也解相忆。是什么意思
- 月下飞天镜 云生结海楼是什么意思
- 月下飞天镜, 云生结海楼。是什么意思
- 月下飞天镜,云生结海楼。是什么意思
- 月下飞头记是什么意思
- 月下香是什么意思
- 月下高低影,风前远近香。是什么意思
- 月下高秋雁,天南独夜猿。是什么意思
- 月不好了是什么意思
- 月不常圆,花难久艳是什么意思
- 月不离我是什么意思
- 月不胜日,时不胜月,岁不胜时。是什么意思
- 月不通是什么意思
- 月个点是什么意思
- 月中是什么意思
- 月中丹桂是什么意思
- 月中人是什么意思
- 月中仙是什么意思
- 月中仙乐是什么意思
- 月中仙子是什么意思
- 月中兔是什么意思
- 月中双桨归。是什么意思
- 月中女神是什么意思
- 月中折挂是什么意思
- 月中折桂是什么意思
- 月中斫桂是什么意思
- 月中桂是什么意思
- 月中桂胭脂店是什么意思
- 月中桂(打花卉名一)玉兔天香是什么意思
- 月中浮白水,雨后对青山。是什么意思
- 月中聚雪是什么意思
- 月中蟾蜍是什么意思
- 月中行是什么意思
- 月中走千步沙 (清)孙渭是什么意思
- 月中雨是什么意思
- 月临双女是什么意思
- 月临寺是什么意思
- 月临花是什么意思
- 月临边草白 天入海云黄是什么意思
- 月临边草白,天入海云黄。是什么意思
- 月临高阁帘无影,风过回廊幕有波。是什么意思
- 月丹是什么意思
- 月主是什么意思
- 月丽于箕是什么意思
- 月举连赤海牙是什么意思
- 月么帝儿是什么意思
- 月之愁是什么意思