生产最优化原则

生产最优化主要包括两个方面的内容，一是投入要素的最优化组合，二是产品的最优组合。
一种变动生产要素的投入量的最优化原则应该考虑两方面的内容： 一是要确定生产的最佳区间 （或说合理的生产阶段）；二是要在最佳区间内寻找变动的投入要素与国家的投入要素结合的最佳点。就第一个内容来说，由于边际收益递减规律的作用，使利润极大化的最佳区间是从平均产量等于边际产量到边际产量为零的这一段区间。平均产量 （某种要素的） 是总产量除以某种要素的投入量，边际产量是指某种投入要素一个单位量的变化而引起的总产量的变化数量。关于第二个内容即最佳组合的确定，首先要明确两个概念： 边际产量收入是指由于每增加一个单位变动的投入要素而增加的产量所能获得的收入；单位产品的边际成本是指单位边际产品所包含的变动的投入要素的价值。根据利润极大化原理，则有。式中MRQ为单位产品的边际收入 (若价格不变，则等于边际产品售价PQ); MCQ为单位产品的边际成本； MQx为x要素的边际产量，Px为x要素的价格。也就是说，一种变动投入要素最优化的投入原则是Px=MRPx（边际产量收入）。它表明变动的投入要素价格等于变动的投入要素的边际产量收入时，企业所能获得的利润极大。
多种变动投入要素的最佳组合即最优化原则，需要用等成本线和等产量线加以说明并辅之以数学推导。等产量线是指在生产量一定的情况下，各种投入要素之间的不同组合而连成一条曲线，曲线上任何一点，其产量均相等。等成本线是在总成本一定的情况下，把它在各种不同的投入要素之间的不同分配连成的一条曲线，曲线上任一点，其成本均相等。等成本线与等产量线的切点上，边际技术替代率等于等产量线的斜率，与等成本线的斜率相等，即MQx/Px=MQy/Py=……=MQi/Pi，这就是多种变动要素投入的最优组合原则 (式中，MQi/Pi表明购买i种投入要素所能获得的边际效益)。它反映的是若购买各要素的边际效益相等，即说明企业投入的资源实现了最佳的组合。
在资源约束的情况下，企业多种产品最优组合的原则的确定，需要借助盒形分析图 (如图H)。该图是由X、Y两种要素组合的，实际上是A、B两种产品等产量线坐标图组合而成，QA为A产品的等产量线，QB为B产品的等产量线，其切点便是A、B两种产品的最优组合。但该图平面上任一点都有两条 (QA和QB) 等产量线通过，这样就有无数个两种产品的最优组合点，这些接合点连接而成一条契约线L。契约线上任一点都表示两种产品的最优组合，这种组合有无数组解，一般称之为帕雷托优解。借助于数学手段，可以证明，两条等产量线相切时，MQAx/MQAy=MQBx/MQBy，即当两种投入要素对于A产品的边际产出率之比等于两种投入要素对于B产品的边际产出率之比时，两种产品便实现了最佳组合，或说得到了帕雷托最优。

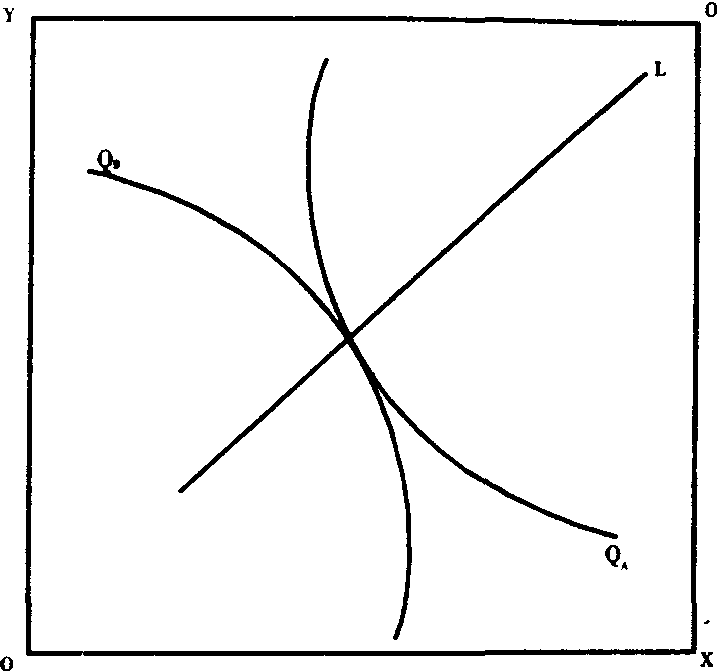
图 H

上述分析说明了帕雷托优解，但每种产品的产出量究竟应为多少才能使企业利润极大化的目标实现的问题仍未解决。这就要求考虑生产者与消费者均衡的产品最优组合。不难证明，当生产可能性曲线（在既定投入要素下可能生产出来的产品组合连成的曲线） 与等收入线 （在保证企业总投入不变的条件下可能的产品组合连成的线性曲线） 相切时，消费者与生产者才能实现均衡。在这个切点上，dy/dx=-Px/Py，即生产的边际交换率等于消费的边际替代率 （等收入曲线的斜率） 时，产品的产量才能实现最优的组合和企业利润极大。