球坐标系
球坐标系qiuzuobiaoxi
又称“空间极坐标系”。设OX,OY,OZ为直角坐标轴,P为空间任意一点,其直角坐标为(x,y,z)它在XY面上的射影是N,又N在X轴及Y轴上的射影分别是A及B (如图所示)。设∠AON=θ,∠NOP=φ,OP= ρ。且规定0≤ρ<+∞,一π<θ≤π,-π/2≤φ≤π/2。那么P点的位置可用一组有序实数 (ρ,φ,θ)表示,这种点和数的对应方法称为球坐标系(或空间极坐标系),三个数ρ,φ,θ称为
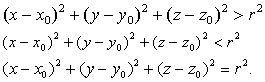
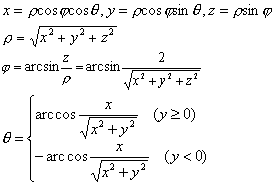
☚ 球面 点与球面的关系 ☛
- 绿沈石是什么意思
- 绿沉是什么意思
- 绿沉枪是什么意思
- 绿沉沉是什么意思
- 绿沚是什么意思
- 绿油是什么意思
- 绿油油是什么意思
- 绿泛蓉池是什么意思
- 绿波是什么意思
- 绿波初涨桃花浪,画鹢轻随柳絮风。是什么意思
- 绿波春浪满前陂,极目连云𫁲䅉肥。更被鹭鸶千点雪,破烟来入画屏飞。是什么意思
- 绿波楼诗集是什么意思
- 绿波波格是什么意思
- 绿波社是什么意思
- 绿波社长沙分社是什么意思
- 绿波细雨伤南浦,红树春风梦若耶。是什么意思
- 绿波荡漾的样子是什么意思
- 绿泥石是什么意思
- 绿泥石玉是什么意思
- 绿泽兰是什么意思
- 绿洲是什么意思
- 绿洲之恋是什么意思
- 绿洲农业是什么意思
- 绿洲凯歌是什么意思
- 绿洲发展与生态环境建设是什么意思
- 绿洲土是什么意思
- 绿洲声屏报是什么意思
- 绿洲大厦是什么意思
- 绿洲柏柏尔人是什么意思
- 绿洲百灵是什么意思
- 绿洲经济论是什么意思
- 绿洼洼是什么意思
- 绿浦是什么意思
- 绿浪是什么意思
- 绿海是什么意思
- 绿海葵是什么意思
- 绿涧支离久,朱门掩映深。是什么意思
- 绿涨春前水,青开雨后天。是什么意思
- 绿涯是什么意思
- 绿液是什么意思
- 绿液预热器是什么意思
- 绿清清是什么意思
- 绿游是什么意思
- 绿湖第一集是什么意思
- 绿湖(第一集)是什么意思
- 绿溪是什么意思
- 绿溪全集是什么意思
- 绿溪诗稿是什么意思
- 绿溶溶是什么意思
- 绿滋是什么意思
- 绿滋馆是什么意思
- 绿滋馆稿是什么意思
- 绿满千岩,浣衣石上,倚风凝伫。是什么意思
- 绿满轩是什么意思
- 绿滨是什么意思
- 绿滴滴儿是什么意思
- 绿漪堂是什么意思
- 绿漪草堂文集是什么意思
- 绿漪草堂題跋是什么意思
- 绿潭渔子钓,红树美人攀。是什么意思