交流电路的复数解法

---

复数法是解交流电路的另一常用方法。

根据尤拉公式e^iθ=cosθ+isinθ或cosθ=R_ee^iθ及sinθ=Ine^1θ，可将上条中的A1(t)及A₂(t)化成

A1(t)=ReA₁₀e^i(ωt^+φ1)，

A2(t)=ReA₂₀e^i(ωt+φ₂)

从而

A(t)=ReA₁₀e^i(ωt+φ1)+ReA₂₀e^i(ωt+φ2)

=Re〔A₁₀e^i(ωt+φ1)+A₂₀^ei^(ωt+φ2)〕

这说明，为了计算A(t)，可先引入复量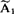及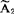

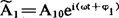
A₂=A₂₀e^i(φt+φ2)

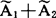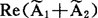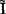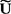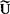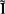尔后先计算，然后从得到A(t)，于是，简谐量的迭加已化为复量的代数运算。引入复电流和复电压的好处还在于可引入复阻抗。例如某段电路上的和的比值

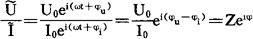
也是一个复数，它的模恰好是该段电路的阻抗Z=U₀／I₀，其中角φ=φ_u－φ_i，若引入复阻抗，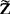

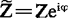
则有

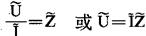
此公式在形式上全同于直流电路中的形式，可见在对待复电压，复电流及复阻抗时，可完全引用直流电路中的相应公式。

对于纯电阻元件R，因有Z_R=R，φ_u－φ_i=0，故知其复阻抗为

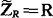
对于纯电容元件C，因有Z_c=1／ωc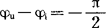，，故其复阻抗为

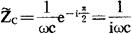
对于纯电感元件L，因有Z_L=ωL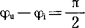，，故其复阻抗为

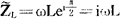
在上述结果的基础上，不难得到其它更复杂一些情况下的结果。

例如，对于N个复阻抗分别为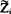的元件的串联电路，因复电流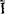是公共的，故各元件上的分复电压分别为

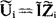，总复电压为

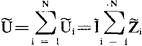
可见该串联电路的总复阻抗。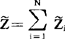

又如对于N个复阻抗分别为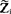的元件的并联电路，因端复电压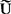相同的，故通过各元件的分复电流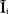应分别为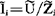，于是总复电流为

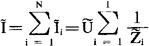
可见该并联电路的总复阻抗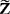满足下面公式

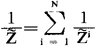
这些结果在形式上全同于直流电路中的相应结果。

对于更复杂的交流电路，作电流、电压、电动势及阻抗的复量计算时，基尔霍夫定律仍然适用。

应该注意，各复量中有物理意义的是它们的模和复角。所以进行复量运算之后，重要的是计算它们的模和幅角，这是比解直流电路复杂之处。