测验等值test equating

测验间的单位系统的转换。包括测验分数等值和试题参数等值两类。等值转换的条件有：测量同一特质；测验的信度相同；测验等值的转换关系具有惟一性、对等性和可递推性。欲等值的测验间存在相互沟通的“桥梁”：共同的试题组或共同的受测者组。

测验等值ceyan dengzhi

指在不同考试分数之间，通过一定的数学模型，把一次考试的分数制转换成另一次考试的分数制。如同温度计中的摄氏制可通过公式F=¹.8C+32换成华氏制一样；通过该式可知，摄氏制(C)上的10°相当于华氏制(F)上的50°；显然，通过该式亦可把华氏制上的度数转换成摄氏制上的度数。进行测验等值时应满足两个条件：
❶所测量的心理特质相同；
❷不同考试的信度相同或相近。测验等值方法主要有：
线性等值 在平行的两次考试中设考试A的原始分数为X，考试B的原始分数为Y，利用它们之间标准分数相等的关系而导出的等值，称为线性等值，即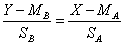

式中 MA、SA——考试A的平均数和标准差MB、SB——考试B的平均数和标准差该式可变为：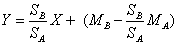

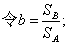
a=^MB-bMA，则上式可变为：

Y=bx+a

[例1] 某中学两年升高中考试的平均数和标准差如下。求这两次考试之间的线性等值关系。

考试 项目	第一年	第二年
平均数 标准差	50.2 13.8	56.1 14.6

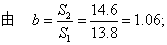
a=M_2-bM₁＝56.1-1.06×50.2=2.9，代入上式得：
Y=1.06X+2.9
这就是两次考试之间的线性等值关系式。
百分位数等值 在平行的两次考试中，利用它们之间百分位数相等的关系而导出的等值，称为百分位数等值。为此，首先要编制各考试的累积次数分布表，然后计累积百分率，最后找出各百分位数所对应的两个考试的原始分数，对应于同一个百分位数的两个考试的原始分数便是等值分数。
铆等值 是在两次考试中均安置一部分共同题目(称为铆题，用U表示)，然后根据两次考试中考生对铆题的反应来调整一个考试的分数。这就称为铆等值。图中，第一次考试有α个考生用X+U部分题目；第二次考试有B个考生用Y-U部分题目，T=α+β，则对

第一次考试

第二次考试
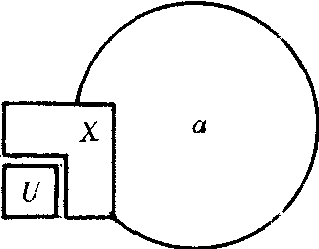
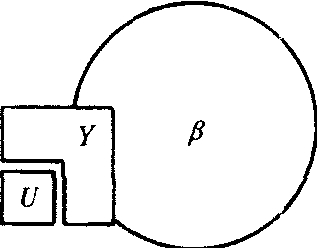
第二次考试分数进行调整的公式如下：

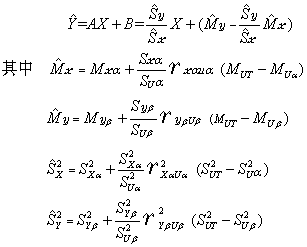
Mx——对考试X调整的平均分
Mxα——考试X的平均分
SXα——考试X的标准差
SUα——X卷上铆题的标准差
TXαUα——X卷上铆题之间的相关
MUT——铆题上全体考生(α+β)得分的平均分
MUα——铆题上α部分考生得分的平均分余类举
[例2] 在两次考试中均使用了铆题U，有关数据如下，求对第二次考试分数调整的等值公式。

考 试	第一次考试		第二次考试		铆题
卷号 项目	Xα	Uα	Yβ	Uβ	UT
平均数 标准差	35.8 5.2	15.5 2.8	41.4 5.3	15.7 2.6	15.8 2.7
相关	0.48		0.54

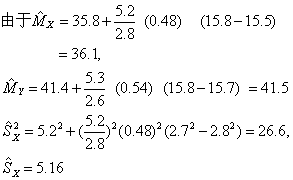
据上式可知，某生在第一次考试中得60分，在铆题上得15分，则Y=1.04×45+4.31=51.1；他在第二次考试中得51.1+15=66.1分。这就是说，第一次考试的60分，相当于第二次考试的66.1分。

测验等值test equating

在教育与心理测验中，把测量同一种心理特质的不同测验版本的测量结果，通过一定数学模型转换到同一单位系统中的过程。即把不同形式测验的分数转换到同一个分数系统上，以解决实际测验中由不同测验形式之间差异所引起的不公平现象。其本质是通过考核同一种心理品质多种形式的测验，设计不同测量分数系统之间的转换模型，进而使这些不同测验形式的测验分数之间具有可比性。测验等值在测验编制、实施、结果分析、分数解释，题库建立、使用和管理，克服时间和空间等因素对测量质量和效果的负面影响方面，都有广泛的应用。