洛伦茨曲线

测量收入或财富分配不平等程度的一条曲线。因20世纪初奥地利统计学家洛伦茨(M.Lorenz)提出而得名。这条曲线把国民收入的百分数看作收入获得者的百分数的函数。

洛伦茨曲线

用统计的方法来描绘测量社会收入在各阶层成员之间分配状况的曲线。如图所示，社会收入分配绝对平均时，则每个人所拥有的收入相等，即人数与收入同比例增加，因此，表现为框形中的45。对角线，如果社会分配绝对不平等，则曲线表示为ABC。但社会上实际的收入分配总是处于这两种极端情况之间，处在低层的人数多而所占有的收入和财富总是较少，相反，富人人数少而占有的收入和财富却多，表现为图中的实际收入分配线。这条收入实际分配线偏离绝对平均线的程度，表明了社会收入分配的不平均程序。洛伦茨曲线也可以成为累进税论所借用的分析工具。它在西方经济分析中应用得比较广泛。

洛伦茨曲线Lorenz Curve

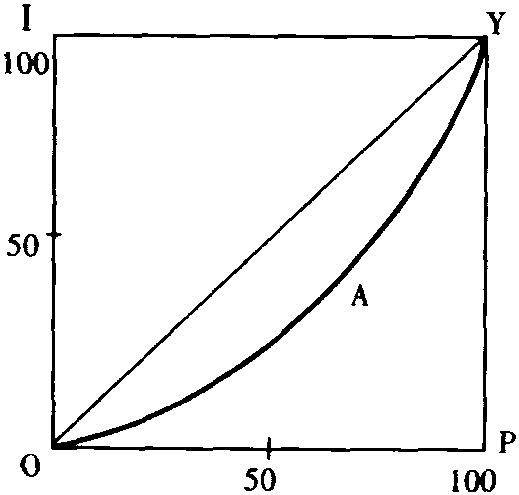
西方经济学用于表示社会收入或财产分配不平均程度的曲线。由奥地利统计学家洛伦茨提出。设下图中OI和OP分别代表累计的收入百分率和累计的人口百分率。正方形OIYP的对角线OY表示收入分配的绝对平均线(Ⅰ)，线上任何点所代表的人口百分率和这部分人的收入在全社会总收入中所占的百分率总是相等的。根据社会收入分配数据描绘出来的OY线(Ⅱ)为洛伦茨曲线，它对收入分配绝对平均线(Ⅰ)的偏离程度越大，表示收入分配不平均的程度越大。如以OI表示一个社会累计的财产百分率，则OY(Ⅱ)线就是表示财产分配不平均程度的洛伦茨曲线。如曲线上A点表示，20%的人口占有收入仅为社会总收入的5%。

洛伦茨曲线

表示社会收入或财产分配不平等程度的曲线。由奥地利统计学家洛伦茨(Lorenz,Max Otto，生卒年不详)提出。图中横轴(OP)表示累计的人口百分比；纵轴(OI)表示累计的收入百分比；对角线(OQ)是绝对平均线，表示占总人数某一百分比的人口恰好拥有相同比例的社会收入；折线OPQ是绝对不平均曲线，表示某一社会成员拥有全部的社会收入，而其他所有人的收入为零。在现实生活中，收入分配的分布曲线(OMQ)即洛伦茨曲线介于绝对平均线和绝对不平均曲线之间，是一条向下弯曲的曲线，其弯曲的程度越大，表明收入分配就越是不平等。用统计方法来表示，可用A的面积(即OMQO)除以A+B的面积(即OPQO)，所得的比率称为“洛伦茨系数”或“基尼系数”。这个系数是由意大利经济学家基尼(Gini,Corrado,1884—1965)依据洛伦茨曲线得出的统计指标。基尼系数介于0和1之间。0表示收入分配绝对平均，1表示收入分配绝对不平均。在0与1之间，基尼系数越小，表示收入的不平等程度越小。

洛伦茨曲线

美国统计学家C·洛伦茨，于1905年设计了一个简便的图式，形象地说明各阶层人口与他们相对收入份额之间的关系，如图：

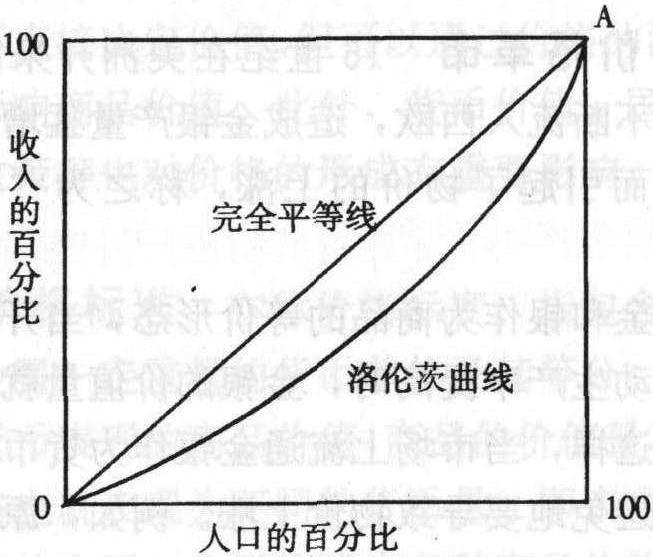
图中，横轴表示收入领取者 （人口） 的数目，按百分比来排列 （由穷到富）,100%时表示全部人口。纵轴表示各百分比人口所获得收入占总收入的百分比，100%表示全部总收入。A点表示全部人口分完了全部总收入。图中OA为45度对角线，对角线上任意一点所对应的人口百分比和收入百分比都相等，因此被称为完全平等线。也就是说每个百分比的人口都得到了同等百分比的收入。实际上任何一个国家也不可能达到对角线所表示的完全平等。洛伦茨曲线显示的就是收入者占总人口的百分比与其所得收入占总收入百分比之间的实际数量关系。洛伦茨曲线与对角线相距越远，也就是洛伦茨曲线的曲率越大，不平等的相对程度也越大；相反，洛伦茨曲线与对角线相距越近，则有相对平等的分配规模格局。

洛伦茨曲线Lorenz Curve

用来表示收入或财富分配不平均程度的曲线。由奥地利统计学家洛伦茨(Max Otto Lorenz)提出。是一种图示手段 （如图），由一个正方形、正方形的对角线以及至少一条连结对角线两端的曲线所组成。正方形的横坐标代表人口数的累积百分比，从0%到100%，纵坐标代表收入 （或财富） 的累积百分比，从0%到100%。连接两对角的直线OY为绝对平均曲线，该线上任何一点表示：总人口中每一定百分比的人口所拥有的收入量在总收入中也占有相同的百分比，该社会的收入分配是绝对平均的。OPY线是分配绝对不平均线，表示全社会的收入都归一人所有，其余人的收入为零。实际收入分配曲线介于绝对平均线和绝对不平均线之间，在此曲线上(OAY)除了起点和终点以外，任何一点到两轴的距离不相等。实际收入分配曲线与绝对平均曲线越接近，社会收入分配越接近平均； 反之，这两条曲线差距越大，社会收入分配越不公平。洛伦茨曲线的方程为：

式中，y>0代表收入水平；P表示人口累积百分比(收入小于y的累计人口占总人口的百分数);I表示收入累积百分数(收入小于y的所有人的累计收入占总收入百分数);ρ(u) 表示收入的密度函数； μ是收入的期望值或社会的平均收入，即：

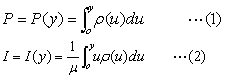
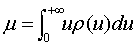
(1)式表示收入小于y的累计人口分布函数；
(2)式表示收入小于y的所有人的总收入的分布函数。

洛伦茨曲线的特征有：(1)P(0)=0,I(0)=0，即0%的人口拥有0%的收入；P(+∞)=1,I(+∞)=1，即100%的人口拥有100%的收入。(2) 其斜率等于收入水平与平均收入之比，且大于零，即：

表示曲线是从原点向右上方上升。(3) 曲线是向下凸的，即：

洛伦茨曲线的明显形式可由方程 (1) 和 (2)导出：

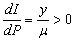
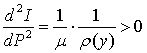
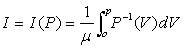
式中P^-1(V)是P(y)的反函数。洛伦茨曲线同计量单位无关，因此用该曲线可对不同地区、不同国家的收入分配情况进行比较；检验政府税收和财政收支的收入分配效应；检验财富分配的不平均程度。如果改变P(y)和I(y)的意义，还可以用来衡量市场结构的垄断程度或物品管理(如ABC法)。洛伦茨曲线的一个缺陷就是绝对平均线并非每个社会都想达到，对不同文化的社会进行比较时，并不能总是准确地反映它们之间的福利差别。
〖参〗基尼系数

洛伦茨曲线Lorenz curve

一种几何图形，它清晰地展现了财富或收入分配的不均等程度及其构成，有时也被用来表示其他变量的分配情况。该图形 （见图） 由一个正方形、一条对角线和一条通过对角线两端点的上凹形曲线所组成。正方形的水平边长代表人口单位的累积份额，从0至100%。垂直边长代表收入（或财富）的累积份额，也是从0至100%。显然，对角线便代表了分配的完全均等化。例如在Z点，占总数30%的人口得到总收入的30%。而对角线下方的曲线则代表了分配的不均等，并且它越远离对角线，不平等程度就越大。

洛伦茨曲线是以它的美国发明者马克斯·奥托·洛伦茨(Max Otto Lorenz) 的名字命名的。洛伦茨将其整个生涯贡献于与分配问题无关的政府统计师工作上，也许是出于偶然，他画出了用横轴表示收入而用直轴表示收入接受者的曲线。 到1921年， 威尔福德·金(Wilford King)在上述基础上画出了现在众所周知的洛伦茨曲线。以后，他通过经济学教科书得到广泛流传。

洛伦茨曲线

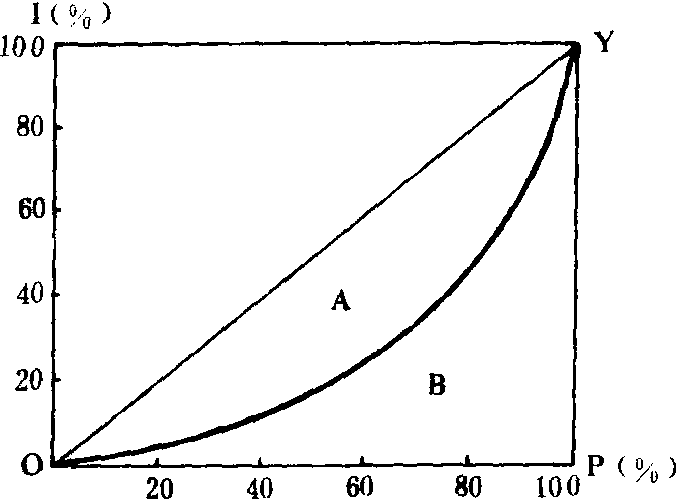
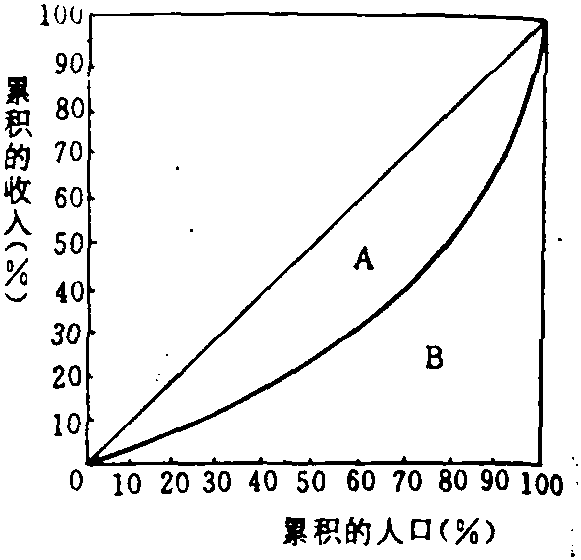
西方经济学家研究分配问题时使用的一种分析工具。由统计学家洛伦茨提出，是用以反映社会收入分配 （或财产分配） 平均程度的一条曲线。如图： 横轴OP代表人口百分比，纵轴OI代表收入的百分比。OY为45°线，称为绝对平等线，意味着每一定百分比的人口获得相同百分比的收入，收入分配是绝对平等的。OPY表示收入分配绝对不平等，最后一个人得到社会总收入的全部。现实经济社会中，反映实际收入分配状况的曲线总是介于上述两种极端之间，该曲线即为洛伦茨曲线。它与OY线越接近，表明收入分配越平等，与OP线越接近，表明收入分配越不平等。根据洛伦茨曲线可以计算出反映收入分配平均程度的指标，该指标称为基尼系数。用A表示上图中实际收入分配线与绝对平等线之间的面积，用B表示实际收入分配线与绝对不平等线之间的面积，则计算基尼系数的公式是： 基尼系数=A/A+B°当A=0时，基尼系数等于0，此时收人分配绝对平等； 当B=0时，基尼系数等于1，此时收入分配绝对不平等。实际的基尼系数总是大于0而小于1的，基尼系数越小，收入分配越平等，反之则越不平等。应用洛伦茨曲线和基尼系数，可以对各国收入分配状况及各种政策的收入分配效应进行比较。例如，把执行某项经济政策 （如增加职工教育支出） 前后的洛伦茨曲线画在同一坐标图上，就可以比较出执行该项政策后对社会收入分配的影响。此外，洛伦茨曲线和基尼系数还可用来分析社会财产分配平均程度的问题。