泰勒公式taile gongshi

若函数f(x)❶在点x₀的某邻域U (x₀)内有定义；
❷在这邻域内有直到n—1阶的导函数；
❸在点x₀处存在n阶导数，f(·) (x₀)，则

f(x)=f(x0) +f′ (x0) (x-x0) +

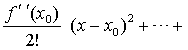
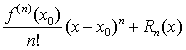
其中

R_m (x) =0 ((z-x₀)ⁿ) (x→x₀).　(2)

式 (1)称为泰勒公式，而R最 (x)的表达式 (2)称为皮亚诺余项.
若函数f (x)❶在闭区间 [ a,b]上有定义；
❷在这闭区间上有直到n阶的连续的导函数；
❸有含有点x0的开区间 (a,b) 内存在n+1阶导函数f(n+1 ) (x)，则

其中

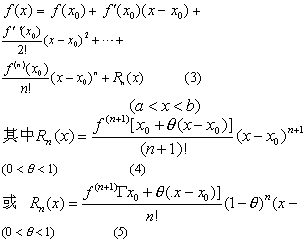
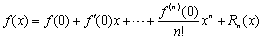(0<θ<1) (4)

或

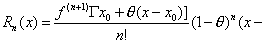x₀ )^m-1(0<θ<1) (5)

公式 (3)称为泰勒公式，式 (4 )称为拉格朗日余项，式 (5)称为柯西余项.
泰勒公式(1),(3)在x₀＝0时，称为麦克劳林公式，即

麦克劳林公式的余项R_m (x) 的表达式有
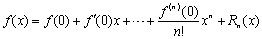
皮亚诺形式： R_m (x) =0 (xm) (x→0)
拉格朗日形式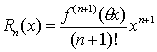：(0<θ<1)
柯西形式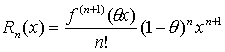：(0<θ<1).
当n=0时，带拉格朗日余项的泰勒公式变成

x)=f(x₀)+f′[_x0 +θ(x -x₀)](x-—x₀) (0<θ<1)

这就是拉格朗日中值定理，可见泰勒公式是拉格朗日中值定理的推广.
泰勒公式是用多项式近似地表示已知函数的重要工具，无论在理论上还是在实际应用上都是重要的.泰勒公式的余项是检验多项式可靠程度的工具，其中拉格朗日余项可解决大部分定量检验的问题.