二项分布

---

描述离散型随机变量的一种常用的概率分布。

设随机变量x表示在n次互相独立的试验中某事件A发生的次数，则事件A发生K次的概率为：

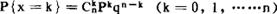
式中：P表示在每次试验中事件A发生的概率；q=1－p，表示在每次试验中事件A不发生的概率。由于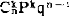正好是二项式(p+q)ⁿ的展开式中的第k+1项，因此这种分布就称之为随机变量x为服从参数n，p的二项分布。二项分布的主要性质如下：二项分布为离散分布，对于固定的n和p，x取k的概率随著k的增大，先是增至最大值，而后再下降；对于固定的p，随著n的增大，二项分布的图形趋于对称；二项分布的数学期望值为np，方差为npq。

二项分布是专门描述每次试验只有发生(或成功)和不发生(或失败)两种可能结果的概率模型，它在生产实践中得到广泛的应用。

例如，某种产品的废品率为1%，如果从一大批这种产品中随机地抽查20个，根据二项分布即可求出这20个产品中废品数是0，1，……20的概率，若求其中有2个废品的概率，则有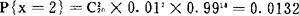。这表明，在进行100次这样的随机抽查中，发现有2个废品的次数仅为1至2次。

由于二项分布概率的计算比较繁琐，所以统计学者已经计算出二项分布概率表供人们查用，见本书附录。