正态性检验

对一个统计量是否服从正态分布所进行的检验即为正态性检验。由于多种统计方法均以样本来自正态总体为基本假定，其使用的效果在相当大的程度上取决于真实总体与正态总体的接近程度，所以正态性检验受到了广泛的重视，其方法也比较丰富，常用的正态性检验有：卡方检验、偏度检验、峰度检验、W’检验、D’Agostina检验、直方图检验、正态纸检验、P-P图检验和Q-Q图检验等。常被应用于测验分数统计中。

正态性检验test of normality

指检验某事物的一组变量值的分布是否符合正态分布。它主要检验频数分布的对称性及是否符合正态峰。根据实际需要可采用正态概率纸法、正态性D检验法及动差法等进行检验。在某些统计处理中，首先应检验其分布是否合乎正态，才能正确选用适当的统计方法。

正态性检验

正态性检验是推断资料是否服从正态分布，或样本是否来自正态总体的统计方法。有些统计方法只适用于正态分布或近似正态分布资料，如用均数和标准差描述资料的分布特征，用正态分布法确定正常值范围等。因此，在应用这些方法时，常要进行正态性检验。
正态分布有两个特征： 对称和正态峰。分布不对称就是偏态。峰偏左，长尾向右侧（即观察值较大一端）伸延的叫右偏态，此时均数与众数之差为正值，故亦称正偏态；峰偏右，长尾向左侧（即观察值较小一端）伸延的叫左偏态，此时均数与众数之差为负值，故亦称负偏态；见图1。图2中虚线是正态峰，两条实线：其一峰态尖峭而尾部伸展，两尾部曲线在正态曲线之上，故尾部面积分布与正态分布相比偏多，而中间部分偏少，叫尖峭峰；另一峰顶平阔而尾部短促，两尾部曲线在正态曲线之下，尾部面积与正态分布相比偏少，而中间部分稍多，叫平阔峰。
正态性检验的方法有两大类： 一是对偏度和峰度各用一个指标来评定，其中矩法效率较高；另一类是仅用一个指标来综括评定，W检验效率较高，它适用于样本含量少于100，有表可查，较为简便。D检验效率也好，不论样本含量多少均适用。正态概率纸检验很简便，适用于作粗略的判断。本条目将分别加以介绍。至于传统的x2检验及Kolmogorov(колмогоров)检验，适用于任意频数分布的拟合优度检验，并非检验正态性的专用方法，效率不够高。单纯作对称性检验的方法如Pearson法与Bowley法均较常用，但对称分布并不都是正态分布，故从略。若要求粗略，资料典型，也可仅从频数表考查分布的对称性。读者可按不同要求选用不同的方法。

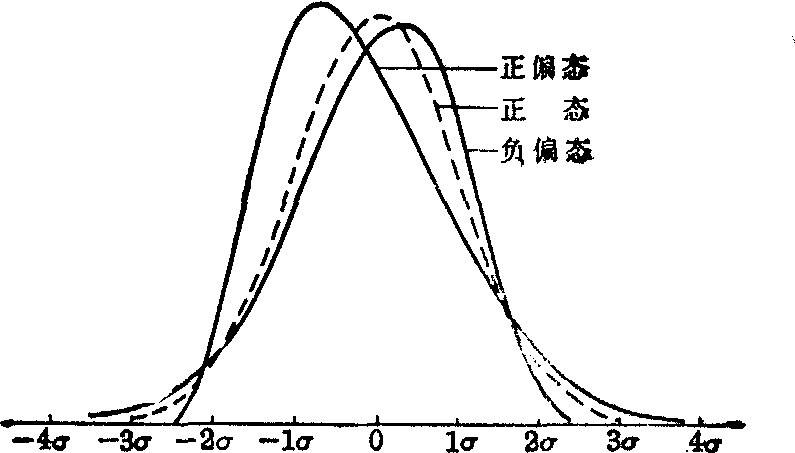
图1 正态与偏态分布曲线

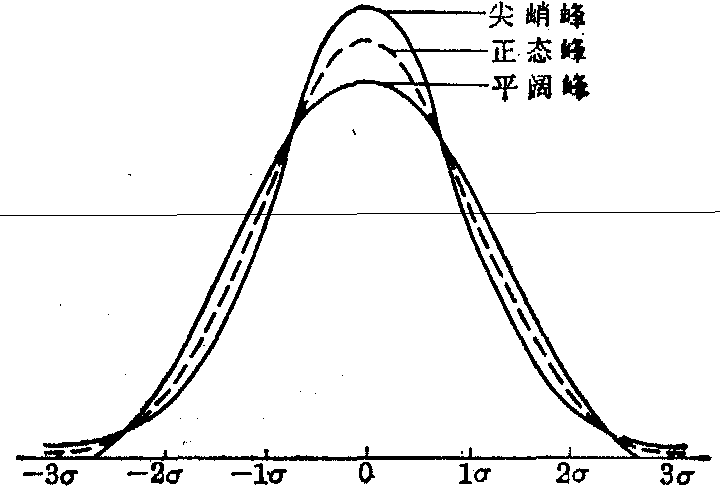
图2 曲线的峰态

矩法 亦称动差法。它是应用数学上矩的原理来检验偏度系数和峰度系数。偏度系数等于0为对称，大于0为正偏态，小于0为负偏态；峰度系数等于0为正态峰，大于0为尖峭峰，小于0为平阔峰。以g1和g2分别表示样本偏度系数和峰度系数，因有抽样误差，故须通过假设检验来作统计推断。方法步骤如下：
(1) 分别按式(1)及式(2)计算g1及g₂。

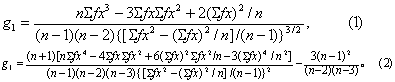
当用频数表计算时，式(1)、(2)中x为缩简值，x=(组中值-假定均数)/组距，f为各组段的频数，n=∑f。这时由于用组中值代替观察值，会引入一定误差，为准确计，可施以Sheppard归并校正。但此校正影响甚微，实际工作中常可省去，因而此处不作介绍。
当用原始数据计算时，式(1)、(2)中x为观察值，f=1,n为样本含量。
(2) 分别按式(3)及式(4)计算g₁及g₂的标准误σg₁及σ_g2。

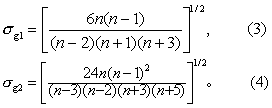
(3)分别按式(5)及式(6)计算ug₁及u_g2。

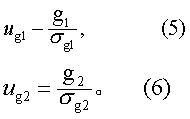
(4)查u界值表得P值，按所取检验水准作出推断结论。
W检验(S. S. Shapiro,M. B. Wilk,1965) 适用于样本含量n≤50时，方法步骤如下：
(1)将n个观察值X_i从小到大依次排列编秩：
X₁ ≤X₂≤…≤Xn,
秩次i=1,2,3，…，n。为简化计算，将观察值从小到大排成两栏，如表4第(2)、(3)栏，第(2)栏自上往下排，第(3)栏自下往上排，这样i=1行，X_i＝X₁＝0.823最小，X_(n-i+1)＝X_n＝1.248最大，两数之差记入第(4)栏，余类推。
(2) 由表1查出当样本含量n确定时的诸系数ai，如表4第(5)栏。当n为奇数时，表1对应于中位数的秩次(n+1/2)的a_i均为0，故中位数可只计秩次，不参加第(6)栏的计算。

表1 正态性W检验用系数ai

n i	2	3	4	5	6	7	8	9	10
1 2 3 4 5	.7071	.7071 .0000	.6872 .1677	.6646 .2413 .0000	.6431 .2806 .0875	.6233 .3031 .1401 .0000	.6052 .3164 .1743 .0561	.5888 .3244 .1976 .0947 .0000	.5739 .3291 .2141 .1224 .0390
n i	11	12	13	14	15	16	17	18	19	20
1 2 3 4 5	.5601 .3315 .2260 .1429 .0695	.5475 .3325 .2347 .1586 .0922	.5359 .3325 .2412 .1707 .1099	.5251 .3318 .2460 .1802 .1240	.5150 .3306 .2495 .1878 .1353	.5056 .3290 .2521 .1939 .1447	.4968 .3273 .2540 .1988 .1524	.4886 .3253 .2553 .2027 .1587	.4808 .3232 .2561 .2059 .1641	.4734 .3211 .2565 .2085 .1686
6 7 8 9 10	.0000	.0303	.0539 .0000	.0727 .0240	.0880 .0433 .0000	.1005 .0593 .0196	.1109 .0725 .0359 .0000	.1197 .0837 .0496 .0163	.1271 .0932 .0612 .0303 .0000	.1334 .1013 .0711 .0422 .0140
n i	21	22	23	24	25	26	27	28	29	30
1 2 3 4 5	.4643 .3185 .2578 .2119 .1736	.4590 .3156 .2571 .2131 .1764	.4542 .3126 .2563 .2139 .1787	.4493 .3098 .2554 .2145 .1807	.4450 .3069 .2543 .2148 .1822	.4407 .3043 .2533 .2151 .1836	.4366 .3018 .2522 .2152 .1848	.4328 .2992 .2510 .2151 .1857	.4291 .2968 .2499 .2150 .1864	.4254 .2944 .2487 .2148 .1870
6 7 8 9 10	.1399 .1092 .0804 .0530 .0263	.1443 .1150 .0878 .0618 .0368	.1480 .1201 .0941 .0696 .0459	.1512 .1245 .0997 .0764 .0539	.1539 .1283 .1046 .0823 .0610	.1563 .1316 .1089 .0876 .0672	.1584 .1346 .1128 .0923 .0728	.1601 .1372 .1162 .0965 .0778	.1616 .1395 .1192 .1002 .0822	.1630 .1415 .1219 .1036 .0862
11 12 13 14 15	.0000	.0122	.0228 .0000	.0321 .0107	.0403 .0200 .0000	.0476 .0284 .0094	.0540 .0358 .0178 .0000	.0598 .0424 .0253 .0084	.0650 .0483 .0320 .0159 .0000	.0697 .0537 .0381 .0227 .0076
n i	31	32	33	34	35	36	37	38	39	40
1 2 3 4 5	.4220 .2921 .2475 .2145 .1874	.4188 .2898 .2463 .2141 .1878	.4156 .2876 2451 .2137 .1880	.4127 .2854 .2439 .2132 .1882	.4096 .2834 .2427 .2127 .1883	.4068 .2813 .2415 .2121 .1883	.4040 .2794 .2403 .2116 .1883	.4015 .2774 .2391 .2110 .1881	.3989 .2755 .2380 .2104 .1880	.3964 .2737 .2368 .2098 .1878
6 7 8 9 10	.1641 .1433 .1243 .1066 .0899	.1651 .1449 .1265 .1093 .0931	.1660 .1463 .1284 .1118 .0961	.1667 .1475 .1301 .1140 .0988	.1673 .1487 .1317 .1160 .1013	.1678 .1496 .1331 .1179 .1036	.1683 .1505 .1344 .1196 .1056	.1686 .1513 .1356 .1211 .1075	.1689 .1520 .1366 .1225 .1092	.1691 .1526 .1376 .1237 .1108
11 12 13 14 15	.0739 .0585 .0435 .0289 .0144	.0777 .0629 .0485 .0344 .0206	.0812 .0669 .0530 .0395 .0262	.0844 .0706 .0572 .0441 .0314	.0873 .0739 .0610 .0484 .0361	.0900 .0770 .0645 .0523 .0404	.0924 .0798 .0677 .0559 .0444	.0947 .0824 .0706 .0592 .0481	.0967 .0848 .0733 .0622 .0515	.0986 .0870 .0759 .0651 .0546
16 17 18 19 20	.0000	.0068	.0131 .0000	.0187 .0062	.0239 .0119 .0000	.0287 .0172 .0057	.0331 .0220 .0110 .0000	.0372 .0264 .0158 .0053	.0409 .0305 .0203 .0101 .0000	.0444 .0343 .0244 .0146 .0049

（续表）

n i	41	42	43	44	45	46	47	48	49	50
1 2 3 4 5	.3940 .2719 .2357 .2091 .1876	.3917 .2701 .2345 .2085 .1874	.3894 .2684 .2334 .2078 .1871	.3872 .2667 .2323 .2072 .1868	.3850 .2651 .2313 .2065 .1865	.3830 .2635 .2302 .2058 .1862	.3808 .2620 .2291 .2052 .1859	.3789 .2604 .2281 .2045 .1855	.3770 .2589 .2271 .2038 .1851	.3751 .2574 .2260 .2032 .1847
6 7 8 9 10	.1693 .1531 .1384 .1249 .1123	.1694 .1535 .1392 .1259 .1136	.1695 .1539 .1398 .1269 .1149	.1695 .1542 .1405 .1278 .1160	.1695 .1545 .1410 .1286 .1170	.1695 .1548 .1415 .1293 .1180	.1695 .1550 .1420 .1300 .1189	.1693 .1551 .1423 .1306 .1197	.1692 .1553 .1427 .1312 .1205	.1691 .1554 .1430 .1317 .1212
11 12 13 14 15	.1004 .0891 .0782 .0677 .0575	.1020 .0909 .0804 .0701 .0602	.1035 .0927 .0824 .0724 .0628	.1049 .0943 .0842 .0745 .0651	.1062 .0959 .0860 .0765 .0673	.1073 .0972 .0876 .0783 .0694	.1085 .0986 .0892 .0801 .0713	.1095 .0998 .0906 .0817 .0731	.1105 .1010 .0919 .0832 .0748	.1113 .1020 .0932 .0846 .0764
16 17 18 19 20	.0476 .0379 .0283 .0188 .0094	.0506 .0411 .0318 .0227 .0136	.0534 .0442 .0352 .0263 .0175	.0560 .0471 .0383 .0296 .0211	.0584 .0497 .0412 .0328 .0245	.0607 .0522 .0439 .0357 .0277	.0628 .0546 .0465 .0385 .0307	.0648 .0568 .0489 .0411 .0335	.0667 .0588 .0511 .0436 .0361	.0685 .0608 .0532 .0459 .0386
21 22 23 24 25	.0000	.0045	.0087 .0000	.0126 .0042	.0163 .0081 .0000	.0197 .0118 .0039	.0229 .0153 .0076 .0000	.0259 .0185 .0111 .0037	.0288 .0215 .0143 .0071 .0000	.0314 .0244 .0174 .0104 .0035

录自 Shapiro SS,Wilk MB:Analysis of variance test for normality (complete sample),Biometrika,52(3 and 4): 591～611,1965 （续表）
(3)按式(7)计算W值，

式中分子部分的∑，当n是偶数时，i=1,2，…n/2；当
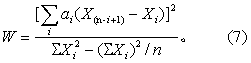
n是奇数时，i=1,2，…(n-1)/2。式(7)的分子即表4第(6)栏合计数的平方，分母中Xi,i=1,2,3，…，n。
(4)得W值后按n查表2得P值，按所取检验水准作出推断结论。
表2 正态性检验用W界值表

样本含量 n	P
	0.05	0.10	0.50	0.90
3 4 5	.767 .748 .762	.789 .792 .806	.959 .935 .927	.998 .987 .979
6 7 8 9 10	.788 .803 .818 .829 .842	.826 .838 .851 .859 .869	.927 .928 .932 .935 .938	.974 .972 .972 .972 .972
11 12 13 14 15	.850 .859 .866 .874 .881	.876 .883 .889 .895 .901	.940 .943 .945 .947 .950	.973 .973 .974 .975 .975
16 17 18 19 20	.887 .892 .897 .901 .905	.906 .910 .914 .917 .920	.952 .954 .956 .957 .959	.976 .977 .978 .978 .979

样本含量 n	P
	0.05	0.10	0.50	0.90
21 22 23 24 25	.908 .911 .914 .916 .918	.923 .926 .928 .930 .931	.960 .961 .962 .963 .964	.980 .980 .981 .981 .981
26 27 28 29 30	.920 .923 .924 .926 .927	.933 .935 .936 .937 .939	.965 .965 .966 .966 .967	.982 .982 .982 .982 .983
31 32 33 34 35	.929 .930 .931 .933 .934	.940 .941 .942 .943 .944	.967 .968 .968 .969 .969	.983 .983 .983 .983 .984
36 37 38 39 40	.935 .936 .938 .939 .940	.945 .946 .947 .948 .949	.970 .970 .971 .971 .972	.984 .984 .984 .984 .985
41 42 43 44 45	.941 .942 .943 .944 .945	.950 .951 .951 .952 .953	.972 .972 .973 .973 .973	.985 .985 .985 .985 .985
46 47 48 49 50	.945 .946 .947 .947 .947	.953 .954 .954 .955 .955	.974 .974 .974 .974 .974	.985 .985 .985 .985 .985

录自 Shapiro SS,Wilk MB: Analysis of variance
test for normality (complete sample),Biome-trika 52(3 and 4): 591～611,1965
另有W′检验(S. S. Sharpiro,R.S.Francia,1972)，适用于50D检验(R. B. D'Agostino,1971) 方法步骤如下：(1) 将原始数据依次排队、编秩，同W检验方法步骤(1)。
(2) 按式(8)计算D值，

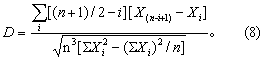
式中符号意义同W检验，式(8)分子算法如表4第(8)栏合计数。
若原始数据一律从小到大依次排列 （不按上述排成两栏），亦可按式(9)计算D值。

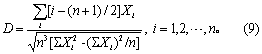
(3) 查表3得P值，按所取检验水准作出推断结论。定P值时，先从表3查到样本含量n (若表中查不到，可用稍大或最相近的n代替)所在的一行，再找到算得的D值在该行的位置，即可得出相应的P值。但应注意：若D值在P=0.20的上、下界之间，则P>0.20。
表3的界值有四位有效数字，故计算D值的过程应至少取五位有效数字，最后精确到四位。正态概率纸检验 方法步骤如下：
(1) 计算累计频率 (%)。有两种情况：
❶对原始数据——先将n个观察值X_i由小到大排列编秩：
X₁≤X₂≤…≤X_n
秩次i=1,2,3，…，n。可仿上述W检验方法步骤(1)，将X_i排在两栏，再按式(10)计算累计频率Fi,

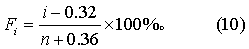
上式计算结果只取整数位，如表4第(9)、(10)栏。注意：表4第(9)、(10)两栏同行相加总和为100，故(10)栏可用倒推法求得较为简便，如第一行，100-3=97。当n为奇数时，中位秩的累计频率必为50%，亦可不必计算，列表时若省去，作图时应补入。
❷对频数表资料——如表5第(1)、(2)栏，须先计算各组段的累计频数，再分别除以n，即得第(8)栏的累计频率。
(2) 将资料标在正态概率纸上。正态概率纸的纵横轴，一为算术尺度(标出观察值的大小，如表4第(2)、(3)栏；表5第(1)栏各组段的上限)，一为概率单位尺度（标出累计频率）。若无正态概率纸，可将累计频率作概率单位变换 (见条目“百分数的概率单位变换”) 如表5第(9)栏，然后将资料标在方格坐标纸上，结果与用正态概率纸相同。
(3) 作出推断结论。若散点基本在一条直线上，则不能否定分布的正态性，若与直线距离较远，则可怀疑数据的正态性。

表3 正态性检验用D界值表

样本含量 n	下 界			上 界
	P:0.05	0.10	0.20	0.20	0.10	0.05
10 12 14 16 18 20	.2513 .2544 .2568 .2587 .2603 .2617	.2573 .2598 .2618 .2634 .2646 .2657	.2632 .2653 .2669 .2681 .2690 .2699	.2835 .2841 .2846 .2848 .2850 .2852	.2843 .2849 .2853 .2855 .2855 .2857	.2849 .2854 .2858 .2860 .2862 .2863
22 24 26 28 30	.2629 .2638 .2647 .2655 .2662	.2670 .2675 .2682 .2688 .2693	.2705 .2711 .2717 .2721 .2725	.2853 .2853 .2854 .2854 .2854	.2859 .2860 .2861 .2861 .2861	.2864 .2865 .2866 .2866 .2866
32 34 36 38 40	.2668 .2674 .2679 .2683 .2688	.2698 .2703 .2707 .2710 .2714	.2729 .2732 .2735 .2738 .2740	.2854 .2854 .2854 .2854 .2854	.2862 .2862 .2862 .2862 .2862	.2867 .2867 .2867 .2867 .2867
42 44 46 48 50	.2691 .2695 .2698 .2702 .2705	.2717 .2720 .2722 .2725 .2727	.2743 .2745 .2747 .2749 .2751	.2854 .2854 .2854 .2854 .2853	.2861 .2861 .2861 .2861 .2861	.2867 .2867 .2866 .2866 .2866
60 70 80 90 100	.2717 .2726 .2734 .2740 .2745	.2737 .2744 .2750 .2755 .2759	.2757 .2763 .2768 .2771 .2774	.2852 .2851 .2850 .2849 .2849	.2860 .2859 .2857 .2856 .2855	.2865 .2864 .2863 .2862 .2860
120 140 160 180 200	.2752 .2758 .2763 .2767 .2770	.2765 .2770 .2774 .2777 .2779	.2779 .2782 .2785 .2787 .2789	.2847 .2846 .2845 .2844 .2843	.2853 .2852 .2851 .2850 .2848	.2858 .2856 .2855 .2854 .2853
250 300 350 400 450	.2776 .2781 .2784 .2787 .2789	.2784 .2788 .2791 .2793 .2795	.2793 .2796 .2798 .2799 .2801	.2841 .2840 .2839 .2838 .2837	.2846 .2844 .2843 .2842 .2841	.2850 .2848 .2847 .2845 .2844
500 600 700 800 900	.2791 .2794 .2796 .2798 .2799	.2796 .2799 .2800 .2802 .2803	.2802 .2804 .2805 .2806 .2807	.2836 .2885 .2834 .2833 .2833	.2840 .2839 .2838 .2837 .2836	.2843 .2842 .2840 .2839 .2838
1000 1250 1500 1750 2000	.2800 .2803 .2805 .2806 .2807	.2804 .2806 .2807 .2808 .2809	.2808 .2809 .2810 .2811 .2812	.2832 .2831 .2830 .2830 .2829	.2835 .2834 .2833 .2832 .2831	.2838 .2836 .2835 .2834 .2833

摘自 Zar JH: Biostatistical Analysis,p 504 Prenti-
ce-Hall,Inc.,1974
例1 某地测得20例20～50岁正常人血浆结合¹²⁵碘-三碘甲状腺原氨酸(¹²⁵I-T₃)树脂摄取比值，如表4第(2)、(3)栏，问此资料是否服从正态分布？
H₀:总体服从正态分布，H₁:总体非正态分布。
a=0.10。

表4 用原始数据以三种方法作正态性检验计算表

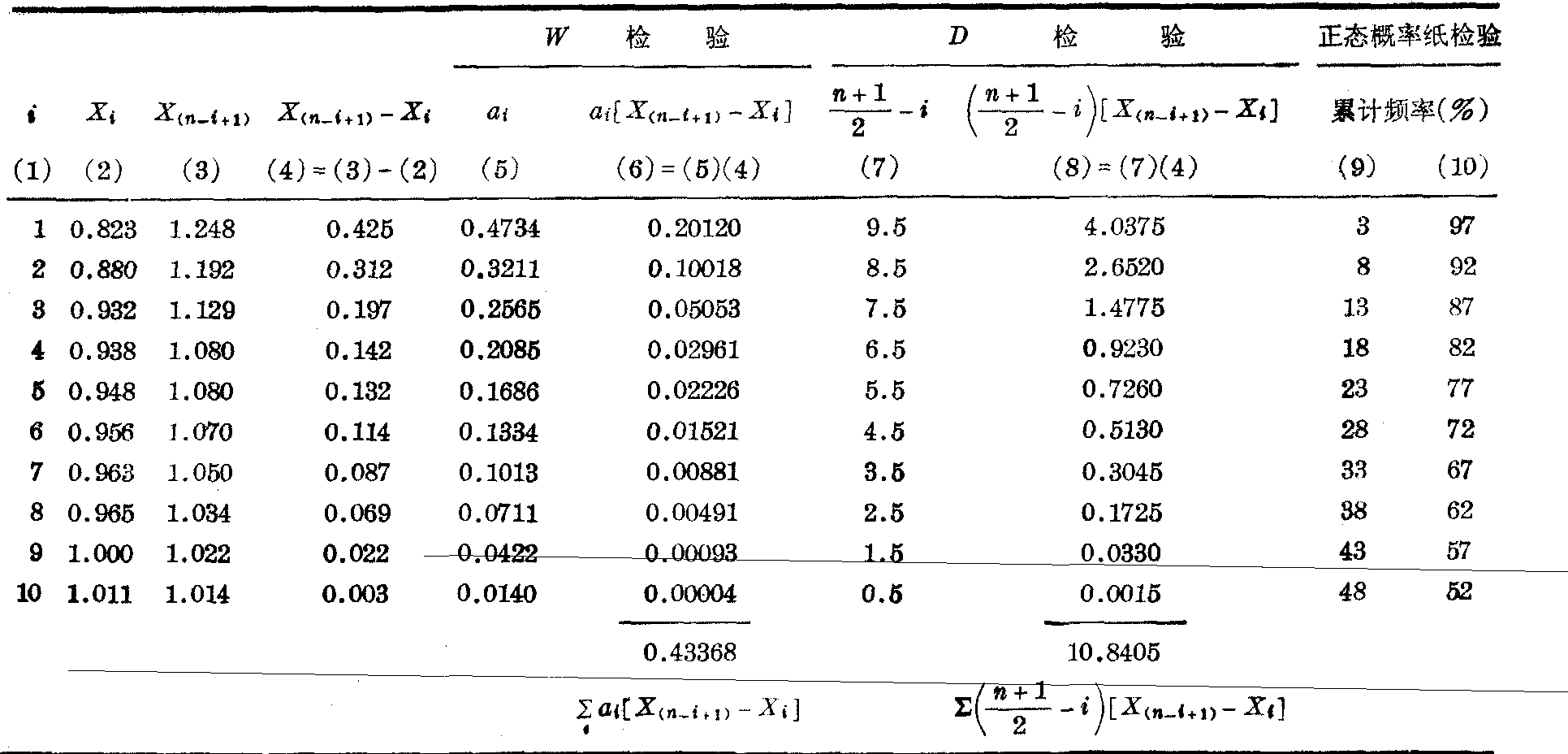
(1)矩法。由表4第(2)、(3)栏资料得n=20,∑X=20.335,∑X2=20.868597,∑X3=21.618669,∑X4=22.609867，代入式(1)～(6)得

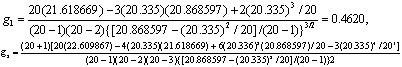
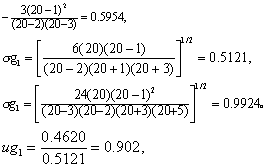
查u界值表得0.50>P>0.20;

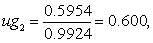
查u界值表得P>0.50。
无论就偏度或峰度检验，按α=0.10水准均不拒绝H₀，可以认为总体服从正态分布。
(2) W检验。今n=20,∑X4=20.335,∑X2i=20.868597，连同表4第(6)栏合计，代入式(7)得

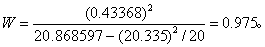
查表2,0.90>P>0.50，结论与矩法一致。
(3) D检验。今n=20,∑Xi=20.335,∑Xi2=20.868597，连同表4第(8)栏合计，代入式(8)得

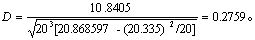
查表3得P>0.20，结论与矩法一致。
(4)正态概率纸检验。将表4第(2)栏与第(9)栏，第(3)栏与第(10)栏的对应点子，标在正态概率纸上，如图3散点，这些点子基本上近于一直线，故可认为此资料服从正态分布。

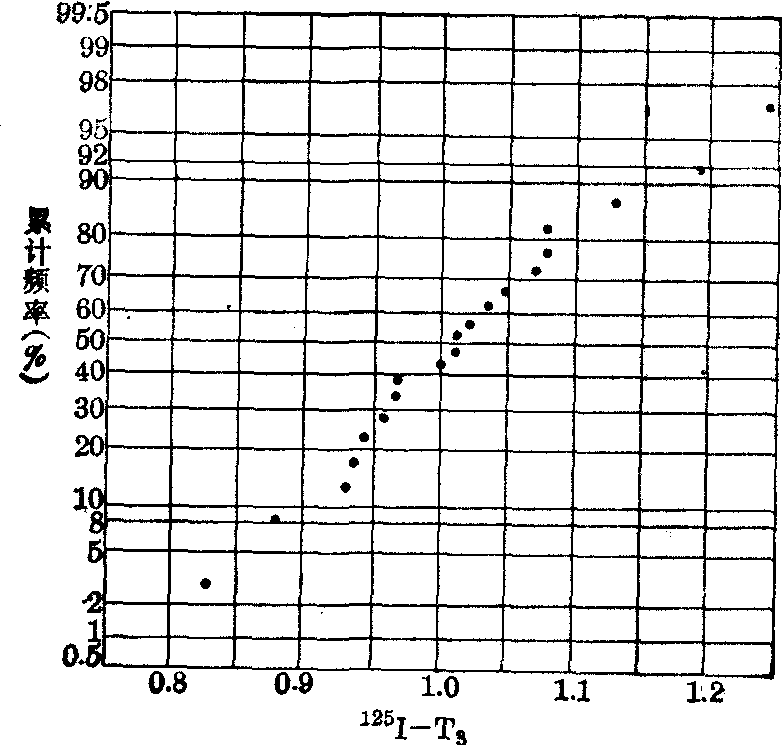
图3 正态概率纸检验

例2 若例1为120例调查资料，经整理成频数表，如表5第(1)、(2)栏，问此资料是否服从正态分布？
H₀:总体服从正态分布，H₁:总体非正态分布。
α=0.10。

表5 用频数表以两种方法作正态性检验计算表

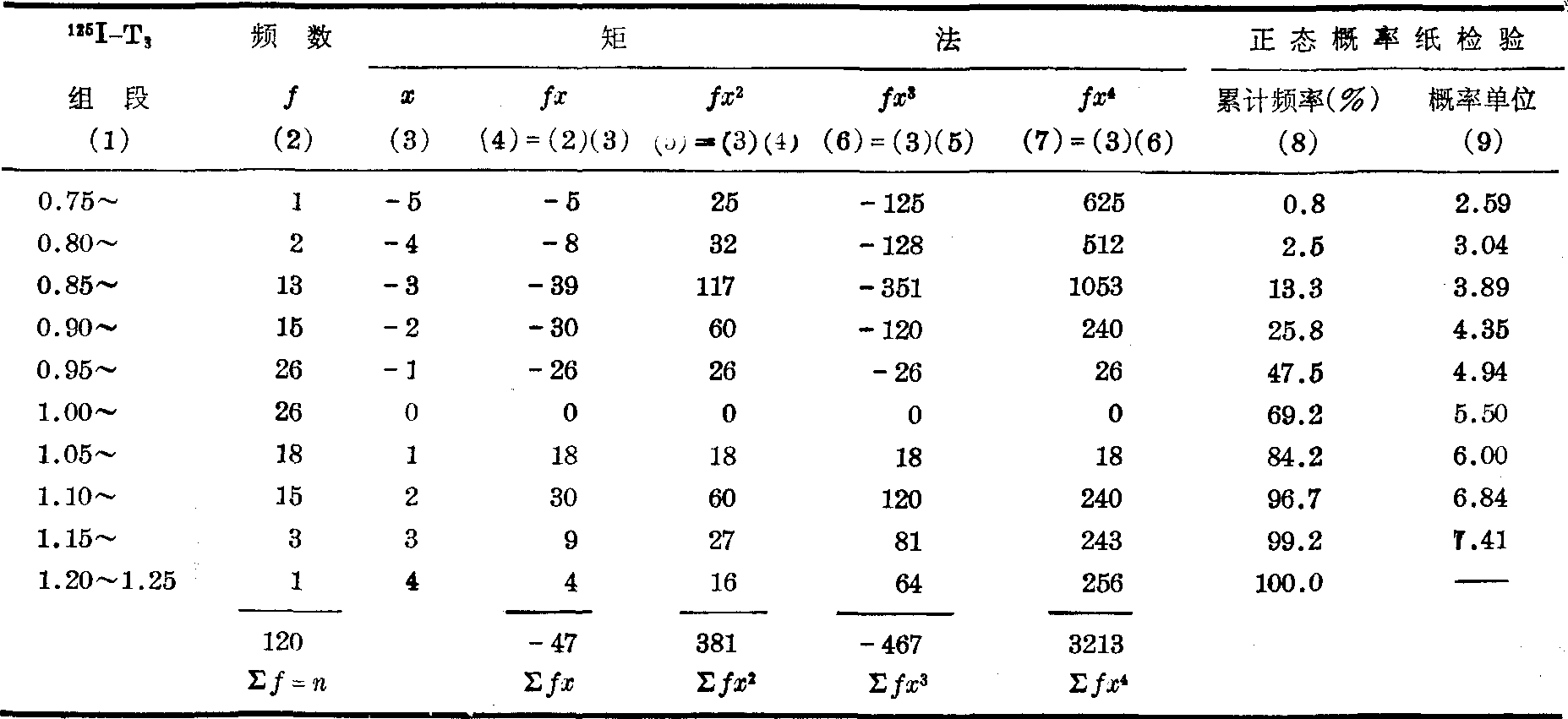
(1) 矩法。将表5第(2)、(4)～(7)栏合计代入式(1)～(6)得

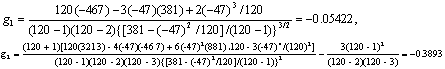
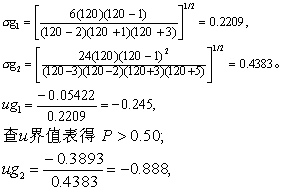
查u界值表得0.50>P>0.20。
无论就偏度或峰度检验，按a=0.10水准均不拒绝H₀，故可以认为总体服从正态分布。
(2) 正态概率纸检验。将表5第(1)栏各上限和对应的第(9)栏数值标在方格坐标纸上，如图4，各散点基本在一条直线上，

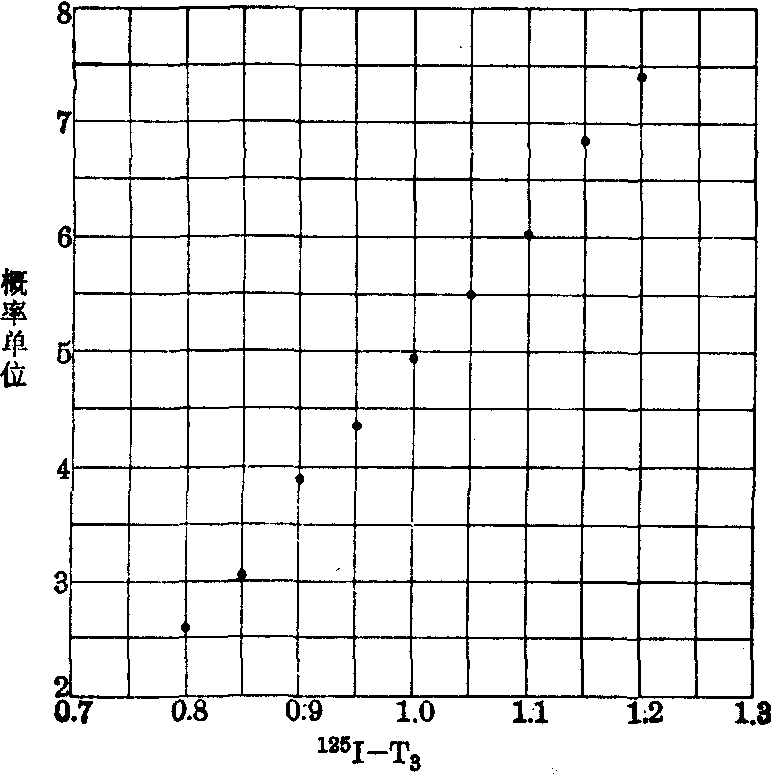
图4 用方格坐标纸作正态性检验

故可以认为此资料服从正态分布。