正交多项式

正交多项式是将多项式回归方程

Y=a₀+a₁X+a₂X²+…+a_kX^k (1)

中的X,X₂，…，Xk进行适当变换，相应地变成ψ1(X),ψ2(X)，…，ψk(X)，于是上述回归方程变为

Ŷ=b₀ψ0(X)+b₁ψ₁(X)+…+b_kψ_k(X), (2)

式中每个ψi(X)是X的i次多项式，亦即ψ1(X),ψ2(X)，…，ψk(X)分别是X的一次、二次及k次多项式。设X是等间隔取值，则可使X₁＝1,X₂＝2，…，X_t＝t，…X_n＝n。如果X_i＝a+h,X₂＝a+2h，…，X_n＝a+nh，则作变换x=X-a/h就可得x₁＝1,x₂＝2，…，x_n＝n;k
为多项式的最高方次，n为样本含量。为简化运算，选择ψi(X)，使

这两条性质称为正交性，可以验证下面一组多项式满足上述正交性。故这组多项式称为正交多项式。
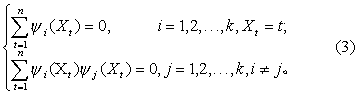
由于Ψ_i(X)(i=1,2，…，k)的值不一定都为整数，为了计算方便，引进适当的系数λi，使
φi=φi(x)=λiΨi(X) ,(5)在n个等间隔点上的值都为整数。对给定的n，相应的λ_i及φ_i在第1,2，…，n各点的数值与s_i＝∑φ²_i都已制成了正交多项式表供实际计算之用，如表1是摘录n为5 ～8的正交多项式表，详表见有关统计表。

表1 正交多项式表(n为5～8 )

t	n
	5				6					7					8
	Φ1	Φ2	Φ3	Φ4	Φ1	Φ2	Φ3	Φ4	Φ5	Φ1	Φ2	Φ3	Φ4	Φ5	Φ1	Φ2	Φ3	Φ4	Φ5
1 2 3 4 5 6 7 8	-2 -1 0 1 2	2 -1 -2 -1 2	-1 2 0 -2 1	1 -4 6 -4 1	-5 -3 -1 1 3 5	5 -1 -4 -4 -1 5	-5 7 4 -4 -7 5	1 -3 2 2 -3 1	-1 5 -10 10 -5 1	-3 -2 -1 0 1 2 3	5 0 -3 -4 -3 0 5	-1 1 1 0 -1 -1 1	3 -7 1 6 1 -7 3	-1 4 -5 0 5 -4 1	-7 -5 -3 -1 1 3 5 7	7 1 -3 -5 -5 -3 1 7	-7 5 7 3 -3 -7 -5 7	7 -13 -3 9 9 -3 -13 7	-7 23 -17 -15 15 17 -23 7
si λi	10 1	14 1	10 5/6	70 35/12	70 2	84 3/2	180 5/3	28 7/12	252 21/10	28 1	84 1	6 1/6	154 7/12	84 7/20	168 2	168 1	264 2/3	616 7/12	2184 7/10

摘自 山内二郎：统计数值表，404,JSA-1972
在多项式回归分析或多项式曲线拟合中，当自变量按等间隔取值时，可利用预制的正交多项式表求各回归系数，使运算过程大大简化，并使不同方次的回归方程的假设检验可以同时进行。
多项式回归分析的方法步骤如下：
(1)根据样本含量n，采用相应的正交多项式表；并按数据描绘的散点图或以往的经验初步确定多项式的方次k (一般k≤5即可，故表中只列出高达5次的正交多项式)；从而列出计算表(如表3)。首先计算

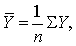
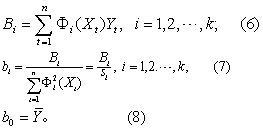
则回归方程为

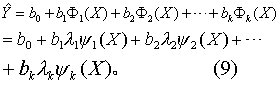
(2)对正交多项式回归进行拟合优度的逐步比较(参见“曲线拟合优度的比较”)。可按表2作方差分析。

表2 正交多项式回归的方差分析

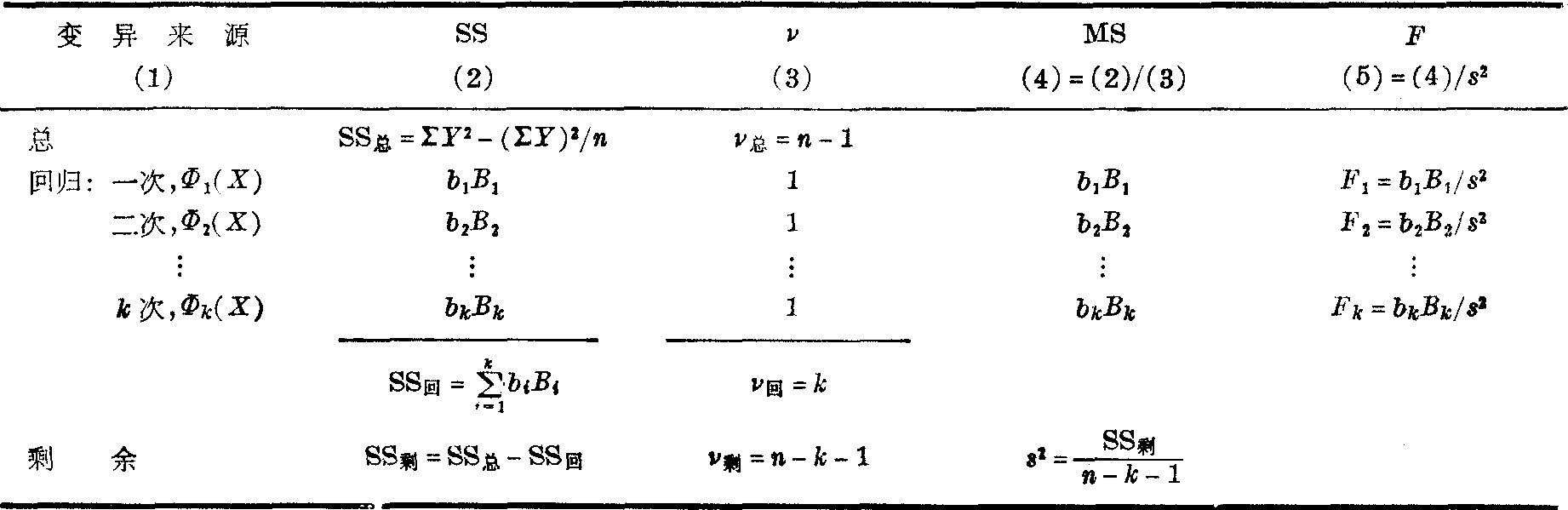
注意：每次多项式φ_i(X)的系数b_i及相应的B_i＝φi(X_i)y_i只与Yt及φ_i(X_t)有关，而不随其他各次多项式的增减而变化。在整个回归分析中，多配一项φi(X)就使回归平方和SS回增加一项biBi。因此可把
b_iB_i＝B_i2/s_i
看作是第i次多项式φ_i(X)的效应，而回归平方和则是各次效应之和。因此检验所配各次多项式Φ_i(X)对Y有无贡献，可用各次效应b_iBi与剩余均方进行F检验，Fi的自由度为1,n-k-1。对于那些没有贡献的高次项可从回归方程中删去。s²之比：

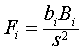
例 不同室温下测定家兔的血糖值，结果如下，试用正交多项式拟合适当的曲线。

温度(℃) X	5	10	15	20	25	30	35
血糖值(mg/dl)Y	130	120	91.5	89	107.5	122.5	147.5

表3 正交多项式计算表

X (1)	x (2)=(1)/5	Φ1 (3)	Φ2 (4)	Φ3 (5)	Y (6)	Y2 (7)
5 10 15 20 25 30 35	1 2 3 4 5 6 7	-3 -2 -1 0 +1 +2 +3	+5 0 -3 -4 -3 0 +5	-1 +1 +1 0 -1 -1 +1	130.0 120.0 91.5 89.0 107.5 122.5 147.5	16900.00 14400.00 8372.25 7921.00 11556.25 15006.25 21756.25
Bi=∑ΦiY		73.5	434.5	-1	808.0 95912.00 (∑Y) (∑Y2)
si bi=Bi/si biBi=B2i/si		28 2.625 192.9375	84 5.173 2247.5030	6 -0.1667 0.1667	n=7 b0=＝808/7 =115.4286
λi		1	1	1/6

表3第(1)、(6)栏为测定数据，第(2)栏系将第(1)栏等差数据简化为1,2，…，7形式。
表3第(3)～(5)栏上半段及si、λi录自正交多项式表(表1)n=7,k=3(由本例散点图可看出各点趋势呈抛物线，即二次曲线，取比它高一次，故k=3)。
表3下半段：Bi按式(6)计算，如

B₁＝(-3)(130)+(-2)(120)+(-1)(91.5)+…+(3)(147.5)=73.5,

余仿此。bi按式(7)计算，如

b₁＝B₁/s₁＝73.5/28=2.625

余仿此。
作方差分析。给定α=0.05，按表2，得

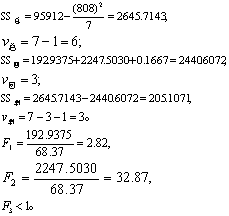
查F界值表得P值，P<0.05者，在F值右上角记“^*”号，按

表4 家兔血糖值的正交多项式回归的方差分析

变异来源	SS	v	MS	F
总	2645.7143	6
回归：一次 二次	192.9375 2247.5030	1 1	192.9375 2247.5030	2.82 32.87*
三次	0.1667	1	0.1667	<1
	2440.6072	3
剩 余	205.1071	3	68.37

a=0.05水准，可认为二次项对Y有贡献，三次项没有贡献。故宜配二次正交多项式，按式(9)及式(4)得

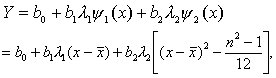
本例由表3，得b0=115.4286,b1=2.625,b2=5.173,λ1=1,λ₂＝1, ＝(1+7)/2=4, x=X/5, n=7。代入方程，并化简得所求的回归方程：

将各X值代入上式可得各相应的估计值Y如下，列出实测值Y以资比较。

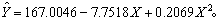
X	5	10	15	20	25	30	35
Y	130	120	91.5	89	107.5	122.5	147.5
Ŷ	133.42	110.18	97.28	94.73	102.52	120.66	149.14

按(X,Ŷ)绘曲线如图，图中黑点是观察值(X,Y)。

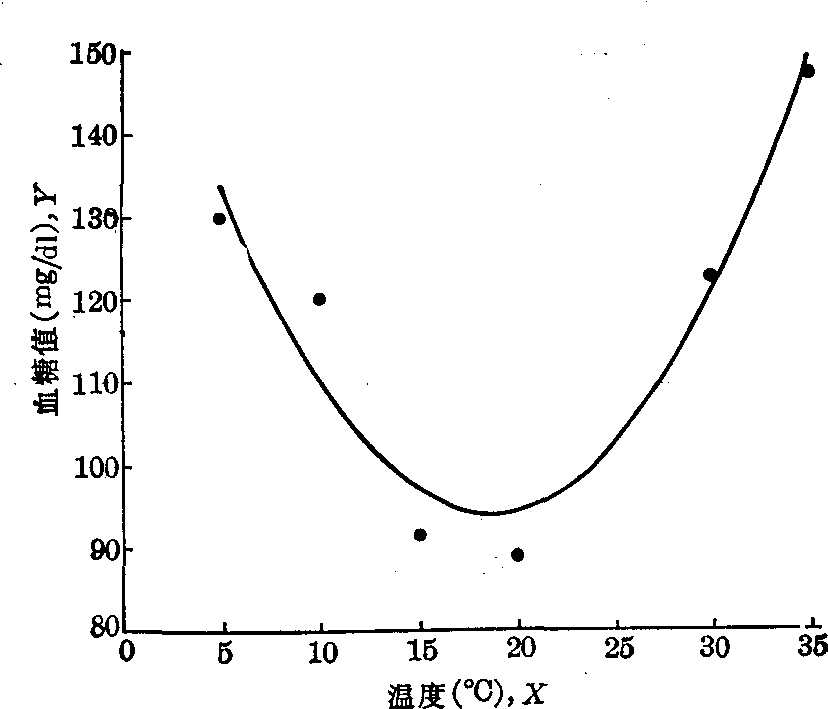
室温与家兔血糖值的关系