欧拉线
欧拉线oula xian
三角形的垂心、外心和重心在一条直线上，这条直线叫做这个三角形的欧拉线.
如图，在△ABC中，H为垂心，O为外心，G为重心.H,G,O三点共线.直线HO就是△ABC的欧拉线.
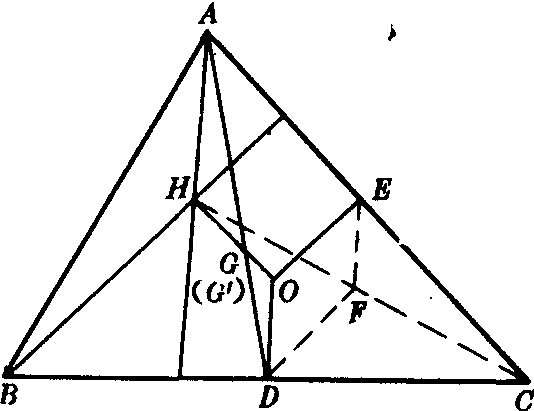
关于H,G,O三点共线简证如下：
证明：D,E分别为BC,AC边中点，作DF∥BH，连FE.则DF∥BH∥OE,F为CH中点，则EF∥AH∥OD.四边形ODFE为平行四边形.则OD=EF=AH/2，若HO交AD于G′，由△G′OD∽△G′HA，知G′D=G′A/2.所以G′与三角形重心G重合.即H,G,O三点共线.
☚ 奈格尔点 三角形的高线长公式 ☛
- 杀火㞘是什么意思
- 杀灭菊酯农药中毒是什么意思
- 杀烈癣药膏是什么意思
- 杀照是什么意思
- 杀熟是什么意思
- 杀熟儿是什么意思
- 杀爬是什么意思
- 杀父之仇是什么意思
- 杀父之仇，不共戴天是什么意思
- 杀父之仇，不共戴天；杀兄之仇，不共日月是什么意思
- 杀父之仇，不可不报是什么意思
- 杀爽是什么意思
- 杀牛是什么意思
- 杀牛族是什么意思
- 杀牛祈祷案是什么意思
- 杀牛祭祖是什么意思
- 杀牲是什么意思
- 杀牲取血祭神是什么意思
- 杀牲畜、家禽等是什么意思
- 杀牲祭祖是什么意思
- 杀牲荐血以祭祀是什么意思
- 杀犬是什么意思
- 杀狗是什么意思
- 杀狗不会，谈狗有余——会谈不会做是什么意思
- 杀狗劝夫是什么意思
- 杀狗劝夫 萧德祥是什么意思
- 杀狗在前，伤人在后是什么意思
- 杀狗记是什么意思
- 杀狗记·雪中救兄是什么意思
- 杀狗赔牛是什么意思
- 杀狠是什么意思
- 杀狠地动是什么意思
- 杀狼地动是什么意思
- 杀猪不吹——蔫煺是什么意思
- 杀猪不吹——蔫煺（退）是什么意思
- 杀猪做豆腐——称不得里手是什么意思
- 杀猪刀子刮胡子是什么意思
- 杀猪匠是什么意思
- 杀猪呼魂是什么意思
- 杀猪哩是什么意思
- 杀猪宰羊是什么意思
- 杀猪宴客是什么意思
- 杀猪捅在屁股上——离心远是什么意思
- 杀猪捅屁股——各有各的杀法是什么意思
- 杀猪教子是什么意思
- 杀猪杀屁股——各有各的办法是什么意思
- 杀猪汉是什么意思
- 杀猪猡容易理肚肠烦难是什么意思
- 杀猪用铅笔刀——全凭决（诀）窍是什么意思
- 杀猪的刀是什么意思
- 杀猪的卖肉——内行是什么意思
- 杀猪的尖刀——身（心）直口快是什么意思
- 杀猪的遇到拦路贼是什么意思
- 杀猪看肝胆卜姻缘是什么意思
- 杀猫令是什么意思
- 杀球是什么意思
- 杀瓜是什么意思
- 杀生是什么意思
- 杀生不如放生是什么意思
- 杀生不如放生。是什么意思