模糊数学方法methods of fuzzy mathematics

一种运用模糊集理论分析和处理模糊性的数学方法。
1965年，美国控制论学者札德(L. A.Zadeh)鉴于复杂系统的复杂性与精确描述之间的矛盾，提出推广经典集合概念，用模糊集合描述复杂事物的模糊性，开辟了数学的新领域。它已应用于医学、气象、生物、农业、林业、专家系统和知识工程等方面，并在冬小麦亲本识别、油橄榄引种分布、小麦赤霉病测报、天气预报等的研究上取得了初步成果。
模糊集理论 经典集合论的基本前提是论域上的元素属于或不属于某个集合。非此即彼，非彼即此。经典集合概念精确地描述了像全体整数、某村庄的全体男人这类清晰事物，但无法描述像老人、青年、丰收、贫困地区这类不清晰事物。因为它们没有确定的外延。现实事物外延的不确定性就叫做模糊性。把模糊性引入集合论，得到模糊集合概念。模糊集合论的基本前提是，承认论域上的元素从属于某个集合到不属于该集合是逐步过渡而非突然改变的。从这一假设出发，把“属于”这个概念模糊化，承认元素可以部分地属于集合，把“属于”概念定量化，引入隶属度概念，把模糊性表述为隶属度的连续渐变性。形式地讲，论域X上的模糊集合A可以通过它的特征函数μ_A来描述，μ_A叫做A的隶属函数。函数值μ_A(x)代表元素X对A的隶属度。μ_A(x)=1=100%，表示X百分之百地隶属于A;μ_A(x)=0，表示X百分之百不属于A，当0<μ_A(x)<1时，表示X部分地属于A,μ值记X属于A的程度。当论域X={x₁,x₂…，x_n}为有限集时，X上的模糊集合A可表示为：

或表示为模糊向量A=(μ₁,μ₂，…，μ_n)。除集合的并、交、补运算均可推广到模糊集合外，还定义了有界和、有界差等模糊集合特有的运算。对给定阈值0≤λ≤1，当μ_A(x)≥λ时，认为相对λ而言X属于A，否则，便不属于A。于是模糊集合A可以用一个经典集合A_λ＝{x|x∈X，且μ_A(x)≥λ}来近似表示，称为A的λ——截集。利用这些基本概念，建立了分解定理、扩张定理、表现定理等基本原理。把经典“关系”概念模糊化，得到模糊关系。论域X到Y的模糊关系R，被定义为直积X×Y上的一个模糊集合，隶属函数为μ_R，函数值μ_R(X,Y)代表有序对具有关系R的程度。当X= {x₁，…，x_n},Y={y₁，…，y_m}时，模糊关系R用一个n×m阶模糊矩阵R=(r_ij)n×m 0≤rij≤1来表示。论域x到Y的模糊关系R与论域Y到Z的模糊关系S的复合，记作R ₀ S，代表模糊关系T,T= R₀ S;μ_T＝ (x,z)= V〔μ_R (x,y)∧μ_s(y,z)〕，∨表示二者之中取大数的运算，如0.6∨0.2=0.6。∧表示二者之中取小数的运算，如0.5∧0.3=0.3。利用模糊集合和模糊关系，可定量描述模糊逻辑和模糊语言。用模糊集合代替经典集合，把现有数学概念(数、微分、积分、概率等)模糊化，可获得新的数学概念，表述新的数学定理。所有这些成果被广义地统称为模糊集理论，构成模糊数学方法的理论基础。
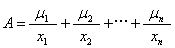
应用模糊集理论解决实际问题的方法主要有以下几种。
模糊聚类分析 依据论域上的模糊等价关系对论域中的元素进行分类的数学方法，是依据经典等价关系把对象划分为若干等价类的传统分类方法的推广。一个关系如果具有自反性、对称性和传递性，称为等价关系；如果它又是模糊的，称为模糊等价关系R，满足以下条件：❶自反性， μ_R(x,x) =1;
❷对称性，μ_R(x,y)=μ_R(y,x);
❸传递性，若μ_R(x,y)≥λ且μ_R(y,z)≥λ，则μ_R(x,z)≥λ。模糊聚类分析包括两个步骤：❶把待分类的对象全体作为论域X，建立从X到X的模糊等价关系（矩阵）R=(r_ij)，作为聚类标准。实际得到的模糊关系往往只有自反性和对称性，不一定有传递性，称为模糊相似关系。需先将相似关系改造为等价关系。用平方法求得相似关系的传递闭包，就是所要求的模糊等价关系。
❷实施聚类。通过取R的λ一截关系Rλ，把模糊等价关系转化为经典等价关系，据之进行分类。令R_λ＝(_ij)，满足：_ij＝1，当r_ij≥λ;_ij＝0，当r_ij<λ。
R_λ是一个以0和1为元素的矩阵。把R_λ中元素相同的各行归为同一类，便得到关于论域X中全体元素的一个分类。不同λ值对应不同的分类结果。根据问题给定的具体条件，确定一个关于聚类水平值λ的序列，1≥λ₁>λ₂>…>λ_k≥0，顺序按R_λ1、R_λ2、…、R_λk分别进行分类，得到一个由细变粗，逐步归并的聚类图。按经典等价关系分类，得到的是一个有严格界限的硬分类，按模糊聚类分析，得到的是一个动态的软分类，能够提供关于对象在不同水平值下的不同隶属关系的全面信息，适用于缺乏明确分类标准的复杂问题。
考虑一个简单例子。设X= {x₁,x₂,x₃,x₄,x₅}，给定X上的模糊等价关系：

取λ=1，得：

5个对象分属5个类别{x₁},{x₂},{x₃},{x₄},{x₅}。取λ=0.8，得：

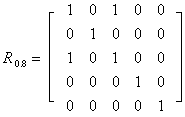
共四个类别{x₁,x₃},{x₂},{x₄},{x₅}。取λ=0.5，得：

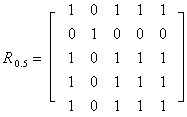
共两个类别{x₁,x₃,x₄,x₅}和{x₂}。若取λ=0.4则5个对象同属于一个类别{x₁,x₂,x₃,x₄,x₅}。
模糊模式识别 用机器模拟人脑思维方式，对事物进行识别和分类，称为模式识别，传统方法以概率论为基础，称为统计模式识别。以模糊数学为理论依据的模式识别，称为模糊模式识别。基本方法有两种，基于最大隶属度原则的直接方法和基于择近原则的间接方法。
直接方法要解决的问题是：待识别的对象是明确的（没有模糊性），模式类型有模糊性，用模糊集合描述，识别就是判明哪个对象优先属于给定的模式，或给定的对象优先归属于哪种模式。又分两种情况：❶最大隶属度原则Ⅰ。给定论域X上的一个模糊集合A（模式），论域中有几个待识别对象x₁…x_n若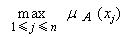。则优先选择x_i。max表示在所有
μ_A(xj)中取最大值。
❷最大隶属度原则Ⅱ。给定论域X上的n个模糊集合A₁…，A_n（模式）,x₀∈X为识别对象，若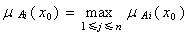，则x₀优先划归A_i。
间接方法要处理的问题是：不但模式类型是模糊的，而且被识别对象也是模糊的，都需用模糊集合描述，模式识别在数学上归结为衡量两种模糊集合的接近程度，按最大接近程度确定对象归属于哪个模式。间接方法的两个主要工具是贴近度概念和择近原则。❶贴近度，一种较简单的定义为：设A、B为论域X上的两个模糊集合，A与B的贴近度为(A,B)=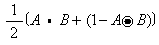,A·B和A⊙B分别代表A与B的内积和外积。
❷择近原则，设论域上给定n个模糊集合A₁，…，A_n（模式），被识别对象为模糊集合B，若ρ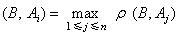，则把B优先划归模式A_i。
聚类分析与模式识别都是一种分类方法。不同的是聚类分析没有事先给定的分类标准（模式），而模式识别是按给定的模式把对象归类的。
模糊相似优先比 模糊决策的一种方法，即根据模糊集理论把对象(生产措施、方案、科研成果、人材等)按某种模糊标准进行排序和择优的方法。给定衡量对象优劣的因素指标，如产量、成本等。设X={x₁，…，x_n}为备择对象集，X_k为比较的样品。x中任二对象x_i和x_j均可与样品x_k成对进行比较，以确定哪个与样品x_k更相似，以便选择与样品相似程度更大者。此方法由两个主要步骤组成，首先建立相似优先比矩阵R=(r_ij)_n×n，满足：r_ij+r_ji＝1。当r_ij＝1时，表示x_i显然优于x_j当r_ij＝0时，r_ji＝1，表示x_j显然优于x_i，当x_ij＝x_ji＝0.5时，表示x_i与x_j的优越程度相同。由于x_i与自身没有比较的必要，规定r_ij＝0,R是X上的一个模糊关系。其次，根据K排序。写出R的各种水平的λ一截矩阵R_λ。令λ从小到大逐步变化，分别检查各R_λ。若第1行中除对角线元素外，在λ由小到大的过程中最先全部达到1，则认为x₁是最优元素。若第m行为次达到1者，则认为x_m是次优元素。依此类推，即可排出次序。对于多指标择优问题，分别写出各指标的相似优先比矩阵，分别排序，然后再作综合处理。一种综合方法是，将分别计算所得单因素的相似程度求和，作为综合的相似程度，依和值的大小最后排定优先次序。有时把这种方法与模糊聚类分析结合使用。
模糊综合评判 应用模糊数学对决策活动所涉及的事物、方案等进行多因素多目标的评价并作出判断的方法，广泛应用于各行各业的管理工作，包括农业生产的管理。评判是由着眼因素（性能指标）和评语构成的系统。实际评判几乎都是多因素的，因素和评语一般都有模糊性，不能用精确数学工具描述。用模糊集合和模糊关系（矩阵）描述因素和评语，用相应的运算描述评判活动，作出带有模糊性的评价就是模糊综合评判。设X={x₁,x₂，…，x_n}为因素集，Y={y₁,y₂，…，y_m}为评语集，X、Y均为有限集。R表示单因素评判矩阵(代表一个从X到Y的模糊关系),A为描述各因素权重的模糊向量，则模糊综合评判的数学模型为模糊变换A⋄R=B，其中B=(b₁,b₂，…，b_m)为Y上的一个模糊集合，或为一个m维模糊向量，代表评判活动所得到的结论。解综合评判问题一般包括三个步骤： ❶求单因素评判矩阵，对于X中给出的各着眼因素，据实际问题的条件作出单因素评判得到n个m维单因素评判向量，以它们为行向量构成的n×m阶模糊矩阵R=(r_ij)，就是所要求的单因素评判矩阵。
❷确定权重集A，根据实际问题给定的条件，确定各因素在被评判事物的总体中的重要程度，用数a_i(0≤a_i≤1)表示因素x_i的权重，构成权重向量A=(a₁,a₂，…a_n)，A需要满足归一化条件
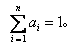
❸作关系复合运算A·R，求出综合评判向量B。通常为便于直观比较，需把B归一化。令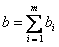，则向量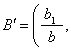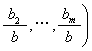代表所论问题的归一化综合评判。以上是综合评判的正问题。
给定单因素评判矩阵R，如果已知综合评判向量B是可以接受的，问相应的权重集合A是什么？这叫做综合评判的逆问题。在数学上，它归结为解关系方程X·R= B，已有多种解法，也可用贴近度来解。给定权重的备择集{A₁, …，A_s}，若ρ(A_i⋄R,B)=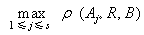，则认为A_i是所求的权重，专家的经验往往表现为善于把握最优权重分配。根据他们给出的评判结论，利用上述方法求出相应的权重集。
模糊规划 目标函数和约束条件中至少有一个是具有模糊性时的数学规划，用于农业管理中技术措施和生产方案的择优等问题。模糊线性规划的数学模型为：
目标函数CX≲Z₀
约束条件AX≲b
非负条件X≥0Z₀为决策人确定的期望值，≲表示模糊小于关系，即大致小于。解模糊规划就是在满足AX大致小于b的约束条件下，使目标函数CX大致小于Z₀。经过适当处理，可转化为普通线性规划问题。模糊规划是普通规划的推广。非线性的数学规划也可推广到模糊情形。选择最优生产方案的模糊规划问题也可以转换为对若干备选方案进行模糊综合评判问题求解。
模糊控制 一种根据模糊集理论制定控制策略的思想和技术，用于复杂的、机理不明的系统。经典控制方法的核心是建立控制系统的精确数学模型，给出精确表述的控制指令。模糊控制的特点和优点是不必建立精确数学模型，只需运用模糊逻辑和模糊语言模拟（表示）人工控制复杂系统的经验，形成模糊指令。人脑制定的控制指令表现为各种模糊条件语句“若A则B”，如“若误差大则阀门关小点”等。以e表示误差，u表示控制量，则误差控制的模糊控制指令可形式地表示为这样一些模糊条件语句： 若e正大，则u负大；若e正小，则u负小；若e为0，则u为0；若e负小，则u正小；若e负大，则u正大。模糊控制过程是制定和执行一系列模糊指令的过程。若适当选取误差论域E和控制作用论域U，把“e正大”、“e负小”等定义为E上的模糊集合，把“u负大”、“u正小”等定义为U上的模糊集合，作为模糊指令的条件语句便可表示为从E到U的模糊关系R:

以实测误差A(E上的模糊集合)作为输入，则输出B(U上的模糊集合)为B=A⋄R模糊控制过程在数学上相当于模糊变换A⋄R。按最大隶属度原则可以确定具体的控制量。把这一系列数学处理交给机器来实现，就能实现模糊自动控制，按这种原理设计的自动控制装置已经问世，如将模糊控制与经典控制适当结合起来，可以达到更好的效果。
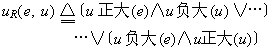
确定隶属函数 应用模糊数学方法解决实际问题的关键是给所涉及的模糊集合建立合理的隶属函数。已经提出的方法有二相模糊统计法、多相模糊统计法、三分法、二级多相模糊统计法、二元对比排序法、判断推理法、示范法、蕴涵解析法、可变模型法、滤波函数法等。

---

模糊数学方法mohu shuxue fangfamethod of fuzzy ma thematics

研究事物模糊性的一种数学方法。是用精确的数学工具， 对概念模糊或者系统复杂难以精确化事物进行测度、运算和逼近的方法。
简况 电子计算机技术的发展促进了模糊数学的出现。1965年，美国控制论专家L.A.扎登首先提出模糊集(Fuzzy sets)概念，形成了模糊集理论，为用数学方法描述事情模糊性提供了手段。1979年陈国范等人首次把模糊数学应用于天气预报业务。此后， 开始用于农业气候区划、地区气候资源评价、作物宜植区的气候选择、产量预报等研究中。现在已显示出其独到的优点。❶是用隶属函数表示农业对象与气象环境因子的关系， 可为其适宜程度提供一个游动边界， 比用传统的指标硬划分， 更符合由量变到质变的客观实际；
❷是通过对隶属函数的确定， 可把因子的原始量测值同对象的反应指标结合起来；
❸是对一些复杂的难以取得精确量测数据的现象， 可用经验公式或定性评分的方法， 使其数量化， 以便计算和分析；
❹是对受多指标变量影响的系统， 可用各指标相应的隶属函数的逻辑复合运算， 模糊关系转换， 得出多因子对对象影响的综合评判值， 这种评判值比加权平均合理，有利于多因子综合分析。
方法 目前使用较普遍的有以下五种方法：
综合隶属函数拟合 这是利用因子隶属函数的软代数运算去拟合对象的方法。首先据经验定出因子模糊子集的边界条件， 以此建立隶属函数， 计算出各因子相应的隶属度， 再作交、并、补等各种软代数组合运算。用所得综合隶属度， 分别对对象模糊子集作拟合判别， 从中选取拟合最优的组合运算， 建立预报方程。优点在于能通过隶属函数的设计， 吸收定性经验到方程中去； 且能通过组合运算， 从原始因子序列中提取较多的信息， 是一种实用而有效的方法。多用于农业气象预报和类型识别。此方法的关键是要设计出一个能合理刻划事物模糊性的隶属函数。常见的隶属函数有正态型、戒上型和戒下型三种， 使用时可根据实际需要选取， 并给出相应的参数值。
模糊模型识别 这是确定被识别对象在已知模型集合中归类的方法。按最大隶属原则， 判别对象在给定模型集中的归属问题， 称为模糊数型识别的直接方法。若被识别对象不是一个确定元素，而是一个子集，则须分别求算对象子集与已知各模型之间的贴近度，再依据接近原则， 确定其归属， 后者即模糊模型识别的间接方法。适用于作物宜植区的气候选择和农业气象预报。
模糊相似分析 这是用模糊集和模糊关系的理论， 决定群分析中相似选择的取舍方法。以引种工作中宜植区的气候选择为例， 原产地和拟引入地的农业气候环境单元，均被定义为气候指标集空间上的向量。则问题便归结为确定拟引入地区中， 某一具体单元和原产地单元的相似较之其它拟引入地单元优先的程度。首先确定能有效地刻划环境单元农业气候特征的因子指标集， 标定在因子空间上两环境单元间的距离（或相似）系数。求算各具体单元相对于其它单元与原产地单元相似的模糊优先比， 建立在选择比配对上定义的拟引入地单元直积空间上的模糊优先比矩阵， 再将矩阵元素由大到小， 依次定作门限水平阈值， 求其水平截集， 则矩阵元素大于阈值者为0, 小于阈值者为1(均对矩离系数而言， 若用相似系数则相反)。若矩阵中某一行， 除主对角线元素外， 在门限阈值由大到小逐步扩展过程中最先全达到1，则该行所代表的单元和原产地单元最相似， 即最优， 对应的阈值为其优先水平。同样， 次达到者为次优， 依此类推。此方法适用于引种气候选择、产量预报的相似型选择。
模糊聚类分析 这是对事物按一定要求进行分类的数学方法， 对其引入模糊数学语言， 便称为模糊聚类分析。模糊等价关系是模糊分类的依据。对样本实行分类，先据需要选取合适的统计量——相似系数（或距离系数），建立样本序列直积空间上的模糊相容关系矩阵， 使矩阵元素归一化，此时关系矩阵具有自反性、对称性， 但不具有传递性。需通过二次幂的连续复合运算， 将模糊相容关系矩阵， 改造为具有自反性、对称性和传递性的模糊等价关系矩阵。再由小到大， 依次选取门限水平阈值， 矩阵元素大于阈值时取值为1，小者则为0。据此模糊等价关系进行截集显示， 其每一水平阈值的截集显示，都可将样本确切地加以分类，得出一系列的不定图象， 即各种不同的分类。
模糊综合评判 这是利用模糊关系变换求算对某一事物的多因素综合评语的数学方法。若因素和评分为有限集， 则可视其从因素集到评语集的模糊关系为一模糊变换器， 根据矩阵的复合运算规则， 任给一个因子着眼点权重的模糊子集， 便可得出一相应的模糊综合评判子集， 即评语向量。通常还需对综合评判向量元素作归一化处理， 便于直观比较。以上是已知输入（因子着眼点权重）求输出（综合评判）, 是综合评判的正问题。若已知输出求输入， 则称谓综合评判的逆问题， 对总结经验中的优越权重分配， 有普遍的实际意义。若将输出改为决策行为的集合， 则综合评判问题就变为综合决策问题。适用于对资源的综合评价和作物引种改制的适区气候选择。