极坐标方程的建立jizuobiao fangcheng de jianli

曲线C和极坐标方程F(ρ,θ)=0满足：
❶曲线上任一点的所有极坐标中，至少有一对适合方程；
❷适合方程的所有数对(ρ,θ)所表示的点都在曲线上.则方程F(ρ,θ)=0叫做曲线C的方程，曲线C叫做方程F(ρ,θ)=0的曲线.
定理 诸方程(F(-1)^kρ,θ+kπ)=0,k∈Z，所代表的曲线完全一样.
推论 曲线C₁:f(ρ,θ)=0，和曲线c₂:g(ρ,θ)=0的所有交点满足
❶若f(0,θ)=0和g(0,θ)=0分别有解，则曲线C₁,C₂有交点是极点(0,0);

❷ 若方程组

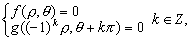
有

解(ρ₀,θ₀)，则曲线C₁,C₂有交点(ρ₀,θ₀).
求曲线的极坐标方程所用的方法与在直角坐标系里的方法基本上相同.
有些点的轨迹问题，用直角坐标方法不易求解时，可考虑适当地引用极坐标法，求它的极坐标方程会使问题变得简单些.