有界数列youjie shulie

如果数列{a_n}的每一项都不大于某一个数M，即a_n≤M(其中n=1,2，…)这样的数列叫上有界数列，或说该数列上有界.其中M叫该数列的一个上界.例如数列

2或3或4均为它的上界.
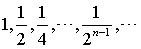
对于一个上有界数列{a_n}，如果存在一个上界β，对任意正数ε，总存在一个正整数N，使a_N>β-ε，则β叫数列{a_n}的上确界.记作Sup{a_n}，上确界是上有界数列的最小上界.例如数列

1是它的上确界.
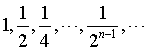
如果数列{a_n}的每项都不小于某一个数m，即a_n≥m，其中n=1,2,3，…，这样的数列叫下有界数列，或说该数列下有界.例如数列

-1或-2或-3均为它的下界.
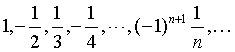
同样的，对于一个下有界数列{a_n}，如果存在一个下界α，对任意正数ε，总存在一个正整数N，使a_N<α+ε，则α叫数列{a_n}的下确界，记作inf{a_n}，下确界是下有界数列的最大下界.例如数列

它的下确界是0.
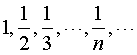
如果一个数列{a_n}既是上有界，又是下有界，这样的数列叫有界数列，或说该数列有界.
一个数列有界还可以这样定义：如果一个数列的每一项的绝对值都不大于某一个正数M，即|a_n|≤M(式中n=1,2,3，…)这样的数列叫有界数列.